Проектирование зеркальных антенн и устройств СВЧ, страница 6

,                              (10)

,                 (11)

где , , - параметр,  - модуль коэффициента отражения волны от раскрыва рупора.

Далее подставив верхние формулы в (10)и(11) получаем:

.

.

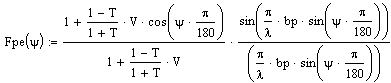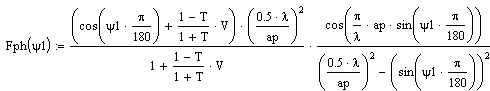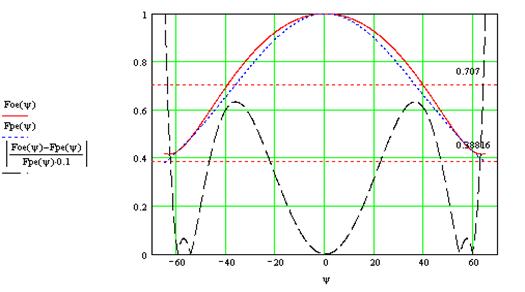
Рис. 10. Требуемая  и реальная ДН облучателя в плоскости Е

 

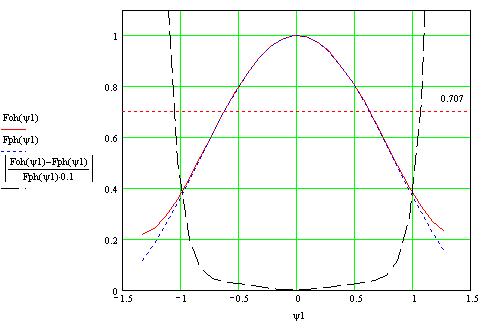
Рис. 11. Требуемая  и реальная ДН облучателя в плоскости Н

Из рис. 10, 11 видно что реальные и требуемые ДН облучателя отличаются не более, чем на 10% ( процентное отличие увеличенное в 10 раз показывает пунктирная кривая), что означает правильность выбора размеров рупора.

Расчет завершается определением положений фазовых центров рупора в главных плоскостях (см. рис. 9):

; .

Расфазировки Ф^Е,Н в раскрыве находят по формулам (9). Подчеркнем два момента. Во-первых, фазовые центры облучателя в плоскостях Е и Н практически совпадают. Расстояние │X_E – X_H │/ 2 между фазовыми центрами должно удовлетворять допуску на смещение фазового центра облучателя из фокуса зеркала вдоль его оси:

                                (10)

Во-вторых, если условие (10) не выполняется, необходимо увеличить длину R_E или R_H и повторить  расчет облучателя.

 В нашем случае X_E = 1.061см, X_Н = 0.906 см,

│X_E – X_H │/ 2 = 0.077 см,     см.

Так как 0.077 < 0.706, допуск на смещение фазового центра облучателя из фокуса зеркала вдоль его оси выполняется.

1.7. Расчет реального распределения поля и ДН зеркала

Расчет проводится для сравнения реального Е_р(x) и требуемого Е(x) распределений поля в раскрыве зеркала. В параболоиде вращения (усеченном параболоиде) с реальной нормированной ДН облучателя  справедливо с точностью до постоянного множителя:

.

После нормировки на максимум получаем расчетную формулу:

.

Здесь величина x определяется по формуле (6),  - по формулам (10) и (11) для плоскости Е и Н соответственно:

, ,;

, .

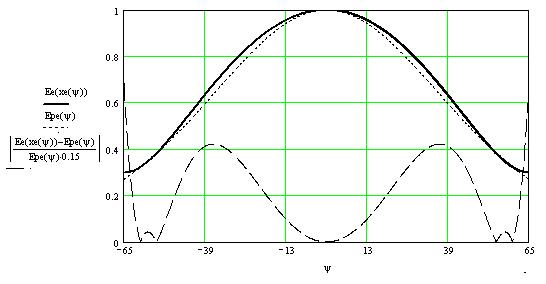
 Рис. 12. Требуемое  и реальное распределение поля в плоскости Е раскрыва