Проектирование зеркальных антенн и устройств СВЧ, страница 3

где a_0.5 – коэффициент пропорциональности, d – размер раскрыва в соответствующей плоскости.

Коэффициент a_0.5 приведен в таблицах для ряда значений D:

D	0.5	0.6	0.7	0.8	0.9
a0.5	63.1	65.7	67.1	70.8	75.9

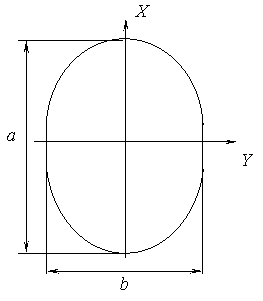
Рис. 5. Зависимость a_0.5 (D)                     Рис. 6. Раскрыв зеркала

Пользуясь таблицей строим зависимость a_0.5(D) (рис.5), по которой зная D находим  и . Далее, пользуясь  заданными значениями частоты f₀ и ширины ДН, определяем размеры раскрыва из формулы (2), учитывая, что l = с / f₀ , где с=3∙10⁸ м/с – скорость света.

В итоге размеры раскрыва в плоскости Е и Н соответственно:

,     м;

,м.

Радиус раскрыва выбираем по большему размеру: R = a / 2.

Так как размеры раскрыва неодинаковы в плоскостях Е и Н, его целесообразно выполнить в виде усеченного параболоида вращения, раскрыв которого показан на рис. 6.

1.4. Расчет ДН облучателя

В параболоиде вращения (или усеченном параболоиде вращения) облучатель должен создавать сферическую волну. У такой волны амплитуда убывает с увеличением расстояния r от источника (облучателя) обратно пропорционально r (в среде без потерь). После отражения от зеркала фронт волны становится плоским, а амплитуда плоской волны в среде без потерь не зависит от расстояния.

Исходя из сказанного выше, связь ДН облучателя f(y) и поля в раскрыве с точностью до постоянного множителя можно записать в виде:

,

где .

Нормируя ДН по максимуму f_макс(y) = r(0) Е(0) = f, получим расчетную формулу для нормированной ДН облучателя:

.      (3)

Из рис. 1 видно, что

,          (4)

.                                (5)

Как следует из соотношений (4) и (5) нормированную координату x в формуле (3) нужно находить по следующей формуле:

.                                       (6)

Значение y₀ выбирают ориентировочно в пределах 50 – 80°. Это дает возможность обеспечить в дальнейшем достаточно высокий КИП при сравнительно небольших размерах облучателя, и как следствие, с меньшим затенением зеркала. С уменьшением y₀ необходимая ДН облучателя может получится настолько широкой, что размеры облучателя станут меньше, чем, например, даже у открытого конца волновода. Зададимся углом раскрыва в плоскости Е: .