Оценка надежности невосстанавливаемых элементов. Оценка надежности сложных систем (с последовательным соединением элементов, с резервированием)

Лекция № 7. Оценка надежности различных систем (2 часа)

1.  Оценка надежности невосстанавливаемых элементов.

2.  Оценка надежности сложных систем (с последовательным соединением элементов, с резервированием).

1.  Оценка надежности невосстанавливаемых элементов

Пусть N - общее число испытываемых или эксплуатируемых объектов (элементов). Пусть за время (или за наработку)  t   отказало  n =  n (t)  элементов.

Тогда количество элементов N_р, оставшихся работоспособными (неотказавшими), будет равно

N_р = N – n(t)  .

Относительное количество отказов

Q(t) = n(t) / N.

Если N  мало, то Q(t) – это оценка вероятности отказа. При N®¥   Q(t) становится вероятностью отказа.

Вероятность P(t)  безотказной работы

P(t)  = N_р /N= (N – n) /N= 1 - n/N= 1 - Q(t).

или

P(t)  + Q(t) = 1.

Это соотношение соответствует тому факту, что отказ и безотказная работа – противоположные (взаимоисключающие) события.

Вероятности отказовQ(t) соответствует функция плотности распределения вероятности наработки до отказа

f(t) = Dn/ NDt = DQ/ Dt ,

где Dn– приращение числа отказавших элементов за наработку (период) Dt .

В пределе получаем

 f(t) = dQ/ dt .

Вероятность отказовQ и безотказной работыP(t)  в функции плотности вероятности f(t) выражаются зависимостями

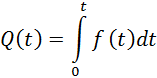
при t=∞

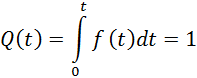
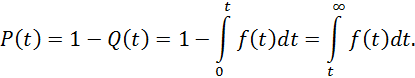
При нормальном законе распределения вероятность отказов равна

Q(t) = F(t) = 0,5 + Ф((t- т_t)/s),

а вероятность безотказной работы

Р(t) = 1 - Q(t) = 0,5 - Ф((t- т_t)/s).

Полученные соотношения могут использоваться и при оценке надежности восстанавливаемых объектов при рассмотрении их работы до первого отказа.

Интенсивность отказов  λ (t) , в отличие от плотности распределенияf(t), относится не к общему числу объектов N, а к числу объектов, оставшихся работоспособными  N_p(см. определение интенсивности отказов):

Интенсивность отказов – показатель надежности невосстанавливаемых объектов, равный отношению среднего числа отказавших в единицу времени или наработки объектов  (N_отк ) к числу объектов, оставшимися работоспособными (N_раб ) .

То есть   λ(t) = Dn/ N_рDt .

Преобразуем это выражение

И окончательно имеем:

2.  Оценка надежности сложных систем (с последовательным соединением элементов,  с резервированием)

Реальные технические объекты – приборы, машины, строительные конструкции являются сложными системами, состоящими из большого (во многих случаях из очень большого) числа элементов (деталей, стыков, соединений, узлов и т.д.).

С точки зрения надежности различают:

-  системы с последовательным соединением элементов;

-  системы с резервированием;

-  сложные комбинированные системы.

Системы с последовательным соединением элементов

Системой с последовательным соединением элементов называется такая система, отказ любого элемента которой приводит к отказу всей системы.

Пример простейшей системы с последовательным соединением элементов – электрическая гирлянда.

Последовательное соединение элементов в такой системе может совсем не соответствовать действительной структуре системы. Например, любая стержневая статически определимая ферма, с точки зрения теории надежности, является системой с последовательным соединением элементов, хотя стержни в такой системе (ферме) могут быть соединены самым сложным  и  разнообразным образом.

Если Р_i (t) – вероятность работы i-того элемента, то вероятность безотказной работы всей системы Р_с будет равна

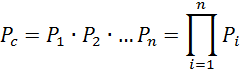
Если то

Последовательное соединение элементов предъявляет жесткие требования к их надежности, иначе надежность всей системы резко падает.

Пусть, например, система состоит из десяти элементов, вероятность безотказной работы каждого равна Р = 0,9. Тогда вероятность безотказной работы системы будет

Р_с = Р ¹⁰ = 0,9¹⁰ » 0,35.

При высоконадежных элементах, когда вероятность их безотказной работы Р близка к единице, а вероятность отказа Q близка к нулю

Р_с =  Р₁´Р₂´ … ´Р_п = (1-Q₁)´ (1-Q₂)´… ´ (1-Q_п) =

= 1 – (Q₁+Q₂+ … +Q_п) + … » 1 – (Q₁+Q₂+ … +Q_п),

так как члены с произведениями Q₂ являются величинами второго порядка малости и их можно отбросить.

Для системы из равнонадежных элементов

Р_с = 1 – пQ.

Так, если система состоит из десяти элементов с надежностью каждого Р = 0,999 и вероятностью отказа Q = 0,001, то надежность системы будет

Р_с = 1 – пQ = 1 - 10´0,001 = 1 – 0,01 = 0,990.

Расчет по точной формуле дает Р_с = 0,990045.

Системы с резервированием

Создание элементов очень высокой надежности для получения надежных сложных систем может быть очень дорого или нереально. В этих случаях для повышения надежности систем используют резервирование.

Резервирование заключается в создании в системе некоторой избыточности. Различают избыточность или резервирование нагрузочное и структурное.