Оценка надежности невосстанавливаемых элементов. Оценка надежности сложных систем (с последовательным соединением элементов, с резервированием), страница 2

Нагрузочное резервирование заключается в создании запасов по нагрузочной способности (например, по грузоподъемности).

Структурное резервирование заключается в ведении в систему резервных составляющих, избыточных по отношению к минимально необходимой структуре системы, и выполняющих те же функции, что и основные элементы.

Основные способы структурного резервирования показаны на схеме.

Если Q_i – вероятность отказа i-того элемента, то вероятность отказа системы равна

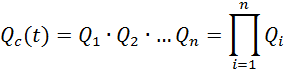
Вероятность безотказной работы системы

P_c (t) = 1 – Q_c (t).

Если элементы в системы равнонадежны, то

Q_c (t) = Q₁^п

и

P_c (t) = 1 –Q₁^п.

Резервирование позволяет значительно повысить надежность сложных систем. Например при п=2 (дублирование) и Q₁=0,1 надежность системы равна

Р_с = 1 - 0,1² = 0,99,

а  при  п = 3 (двойное дублирование)

Р_с = 1 - 0,1³ = 0,999.

Резервирование даже с малонадежным резервом позволяет повысить надежность системы. Пусть элемент с Р₁ = 0,9 и Q₁ = 0,1 мы дублируем малонадежным элементом  Q₁ = 0,5.  Тогда вероятность отказа такой дублированной системы будет

Q_с = 0,1´0,5 = 0,05,

а вероятность безотказной работы

Р_с = 1 – 0,05 = 0,95.

Надежность систем с резервированием зависит от характера резервирования.

Рассмотрим в качестве примера систему из пяти последовательно соединенных элементов с  Р₁ = 0,9  и  Q₁ = 0,1.

Надежность такой системы

Р_с = Р₁⁵ = 0,9⁵ = 0,59,

а вероятность отказа

Q_с = 1 – 0,59 = 0,41.

Введем резервирование в виде такой же системы элементов.

Вероятность отказа такой дублированной системы

Q_с = 0,41²  = 0,17,

а вероятность безотказной работы

Р_с = 1 – 0,17 = 0,83.

Сделаем независимое дублирование каждого элемента.

Вероятность отказа каждого дублированного элемента

Q = Q₁² = 0,1²  = 0,01.

Вероятность безотказной работы системы

Р_с = (1 – Q)⁵ = (1 – 0,01)⁵ = 0,95  >  0,83.