Другие предметы \ Надежность технических систем

Детерминированные способы оценки надежности. Полувероятностные способы оценки надежности. Вероятностный способ оценки надежности, страница 4

f(F)

f(F)

w1

 

 


w2

 

0

F*             F

0

             Ф*                                  Ф

Если F* – некоторое заданное значение случайной величины F, то площадь w1 – это вероятность того, что значение случайной величиныF будет больше F*, то есть

w1 = Р (F>F*).

Если Ф* – некоторое фиксированное значение случайной величины Ф, то площадь w2 – это вероятность того, что значение несущей способности Ф окажется меньше требуемого Ф*, то есть

w1 = Р (Ф < Ф*).

Так как F и Ф, будучи сравниваемы, измеряются в одних и тех же единицах, то их можно изобразить на одном графике.

 


f (F),

f (Ф)

            f (F)                            f (F)

w2w1                       w3

 

0

sF

   F*=Ф*

sФ

F, Ф

В предельном состоянии резерв прочности Z= 0, то есть F = Ф. Этому случаю на графике соответствует точка пересечения кривых f(F) и f(Ф). При этом указанные площади w1, w2,w3 будут равны соответственно:

w1

–  вероятность появления нагрузки, большей, чем F*, а так как мы рассматриваем случайF = Ф, то это вероятность появления разрушающей нагрузки, то есть нагрузки, превышающей Ф*;

  

w2

–   вероятность того, что F* < F*,  а так как  рассматривается  случай   F = Ф, то это вероятность того, что несущая способность окажется меньше заданной нагрузки, то есть вероятность разрушения;

  

w3

–  вероятность неразрушения, то есть надежность.

Если надежность недостаточна, надо или увеличить несущую способность (при этом кривая f(Ф) смещается вправо)  или  уменьшить нагрузку (при этом кривая f(F) смещается влево).

В рассмотренном выше описании не учитывался фактор времени. На самом деле F и Ф изменяются во времени: из-за развития транспорта изменяется характер нагрузки и режимы загружения, возникает коррозия металла, изменяются физико-механические характеристики бетона, возникают усталостные повреждения и т.д.

F,

Ф


0

Т

Поэтому вид выражения, определяющего надежность

Р ((Ф – F) > 0) = Р (Z > 0) ³ Рн ,

становится более сложным и должен быть записан в виде

Р (Z(t) > 0) = Р ((Ф(t) – F(t)) > 0) ³ Рн .

Вероятность безотказной работы сложной системы, например, строительной конструкции, может быть найдена по вероятностям безотказной работы ее отдельных элементов в зависимости от структурной схем системы. Например, при последовательном соединении элементов, когда система теряет работоспособность (переходит в предельное состояние) при отказе хотя бы одного элемента, ее надежность будет

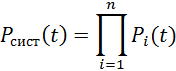
где

i – номер элемента в системе;

Рi(t) – вероятность безотказной работы (надежности) i-того элемента;

п – число элементов в системе.

В настоящее время непосредственные расчеты по изложенной методике (то есть непосредственно вероятностные расчеты) не ведутся из-за крайне недостаточных статистических характеристик по свойствам материалов, величинам нагрузок, влияния технологических факторов, точности монтажа, величинам нагрузки и т.д., тем более с учетом фактора времени.

Расчеты на надежность в более явном вероятностном виде стали использовать при оценке эксплуатируемых сооружений.

Скачать файл