Детерминированные способы оценки надежности. Полувероятностные способы оценки надежности. Вероятностный способ оценки надежности, страница 3

В расчетах обычно пользуются не нормативными R_n, а расчетными R сопротивлениями материалов, определяемыми по формуле

R = т₁R_n / g_т .

Большинство величин, входящих в расчетные формулы (нагрузки, частные коэффициенты условий работы), являются случайными величинами и назначаются с позиций теории вероятности и теории надежности. Однако при расчетах используются конкретные детерминированные значения, полученные на основе указанных теорий, которые фактически  и  используются в нормах, но не в прямом, а в неявном виде. Это дает основание считать метод расчета по допускаемым напряжениям  полувероятностным  методом.

3. Вероятностный способ оценки надежности

И детерминистические, и полувероятностный способы оценки надежности аналитически выражаются одинаково:

F £ Ф,

или в простейшем виде

s £ R.

При этом определяется максимально возможное значение фактора нагрузки (усилия в сечении или элементе) F и сравнивают его с минимально возможным значением Ф.

Вероятностный, случайный характер свойств материала, параметров сечений, загружения, других факторов либо не учитывается вовсе (в детерминистических методах), либо учитывается косвенно на стадии назначения значений расчетных коэффициентов (в полувероятностных способах расчета по предельным состояниям).

Модель обеспечения надежности при этом может быть графически представлена следующим образом.

Очевидно, что наиболее полно и правильно случайный характер (статистический характер) факторов, определяющих значение усилия F (нагрузки) и несущей способности Ф (геометрических параметров сечения и прочности материала) может быть отражено при вероятностном подходе к методике расчета.

Если рассматривать величиныF и Ф как вероятностные, определяемые случайной природой факторов, определяющих их реализацию, то условие надежности может быть представлено в виде

Р ((Ф – F) > 0) = Р (Z > 0) ³ Р_н ,

гдеZº Ф - F – резерв прочности;

 Р (Z > 0) – вероятность положительного значения резерва прочности;

 Р_н – нормированное значение вероятности безотказной работы (надежности).

Очевидно, что при  Z³ 0 система находится в работоспособном состоянии, а при Z< 0 наступает отказ.

Кривые распределенияF и Ф определяются природой входящих в них величин. В частности, статистическое распределение железнодорожной нагрузки близко к нормальному закону распределения, а автодорожной к распределению Пуассона. Прочностные характеристики материала описываются нормальным законом распределения.

Выберем фиксированное число λ > 0 и определим дискретное распределение, задаваемое следующей функцией вероятности:

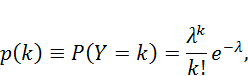
где

·  k!  обозначает факториал,

• e=2.718281828…— основание натурального логарифма.

Тот факт, что случайная величина Y имеет распределение Пуассона с параметром λ, записывается:

Рассмотрим кривые распределения случайных величин F и Ф.