Министерство образования Российской Федерации
Сибирский государственный аэрокосмический университет
имени академика М. Ф. Решетнева
Факультет информатики и систем управления
«Модуляция QPSK»
Лабораторная работа.
Красноярск
2006
Цель работы: Ознакомиться с квадратурной фазовой модуляцией(ФМ-4), принципами ее работы. Научиться модулировать сигнал посредством ФМ-4.
Краткие теоретические сведения:
При двоичной фазовой модуляции один канальный символ может переносить один передаваемый бит, т.е. длительность Ткс=Тс(Ткс – длительность одного канального символа, Тс – длительность символа). Однако, один канальный символ может переносить и большее число информационных бит. Например, пара следующих друг за другом битов может принимать 4 значения: 00, 01, 10, 11. Если для передачи каждой пары использовать 1 канальный символ, то потребуется 4 канальных символа: S0(t), S1(t), S2(t), S3(t), т.е. М=4. При этом скорость передачи символов будет в два раза ниже, чем скорость поступления информационных бит, т.е. каждый Ткс=2Тс.
При фазовой модуляции в качестве канальных символов можно выбрать следующие радиосигналы:
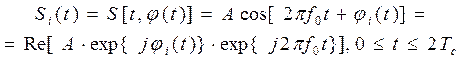
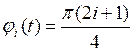
Сигнальное созвездие- отображение сигнала на комплексной плоскости.
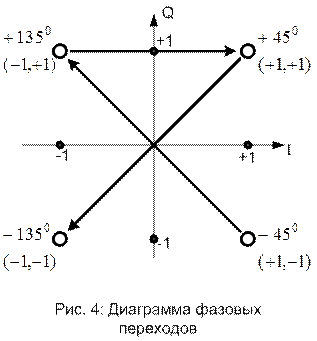
Каждая группа из двух битов представляется соответствующим фазовым углом, которые отстоят друг от друга на 900, а каждая сигнальная точка отстоит по действительной и мнимой части на 450.
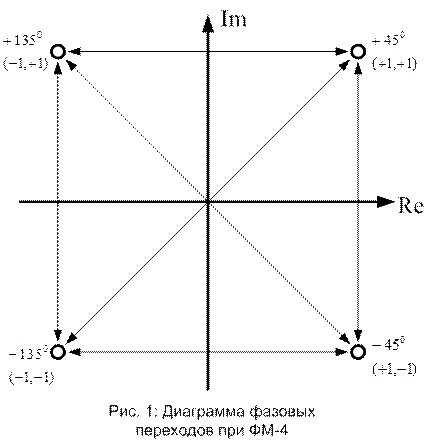
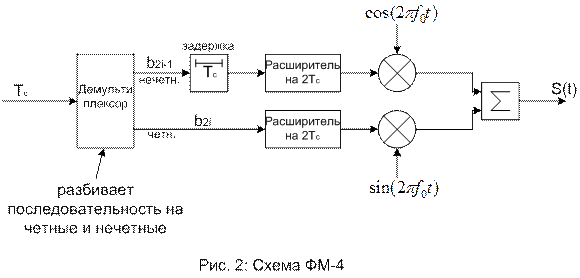
Реализация ФМ-4:
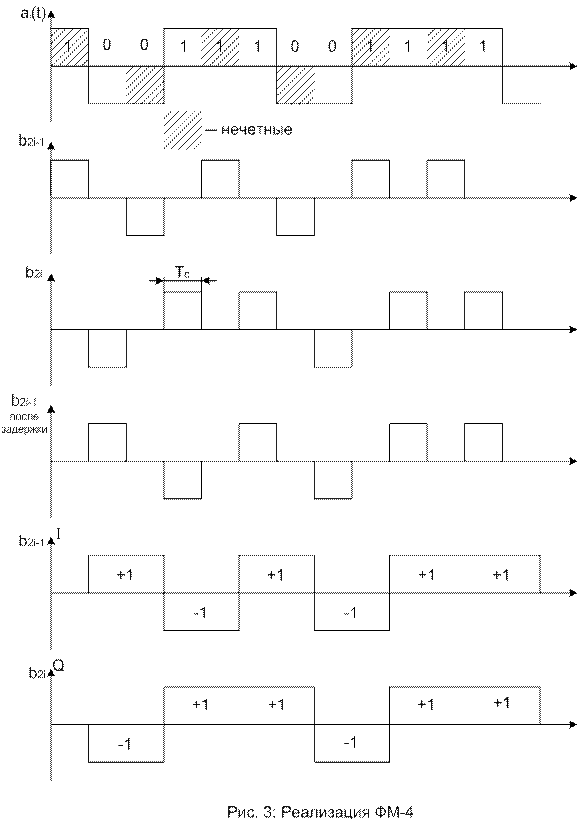
Последовательность передаваемых битов разбивается на две последовательности( четных и нечетных битов). Биты с одинаковыми номерами в этих последовательностях образуют пары, которые удобно рассматривать как комплексные биты. Действительная часть – бит нечетной последовательности, а мнимая часть – бит четной последовательности. Полученные таким способом комплексные биты преобразуются в комплексную последовательность прямоугольных электрических импульсов длительностью 2Тс, которые используются для модуляции несущего колебания. Так образуется сигнал ФМ-4.
Рассмотрим один комплексный бит:
Обозначим символом I значение электрического импульса, полученного из действительной части этого бита, а Q значение электрического импульса, полученного из мнимой части.
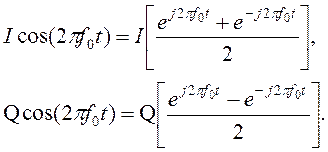
Тогда формируемый ФМ-4 сигнал:
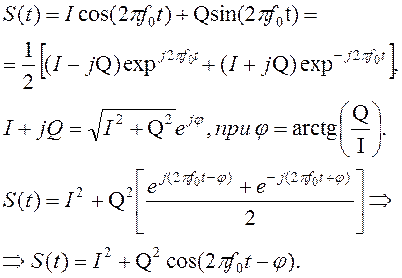
Меняя значения I и
Q, можно получить как амплитудную, так и фазовую
модуляцию. Если принять, что I и
Q принимают значения ![]() , то амплитуда этого сигнала постоянна и
равна
, то амплитуда этого сигнала постоянна и
равна ![]() . А фаза принимает значения: -450,
+450, +1350, -1350.
. А фаза принимает значения: -450,
+450, +1350, -1350.
В результате для комплексной амплитуды высокочастотного сигнала с такой модуляцией можно записать:
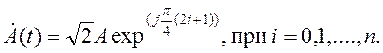
Пример:
Порядок выполнения работы:
1. Ознакомиться с теоретическим материалом.
2. Зайти в Matlab, вызвать библиотеку, написав в диалоговом окне commlibv1: 
3. В
появившемся окне открыть Modulation, дважды щелкнув на
нем: 
4. Далее в
появившемся окне выбрать Digital Modem: 
5. Потом
открыть More function blocks: 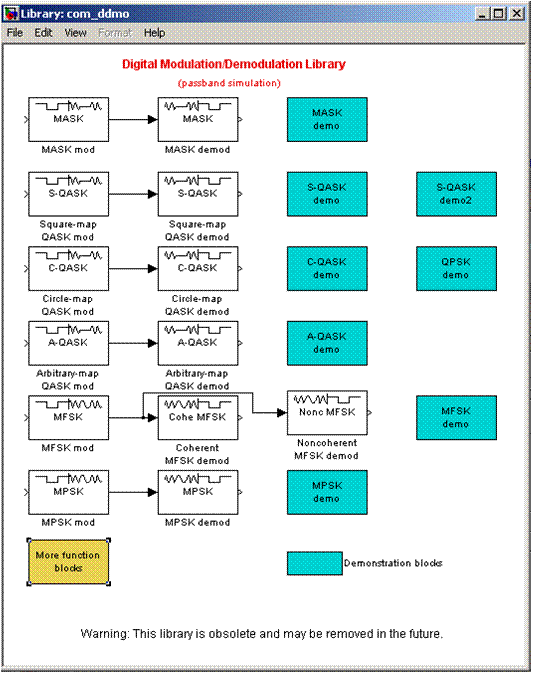
6.
Открыть QPSK demo: 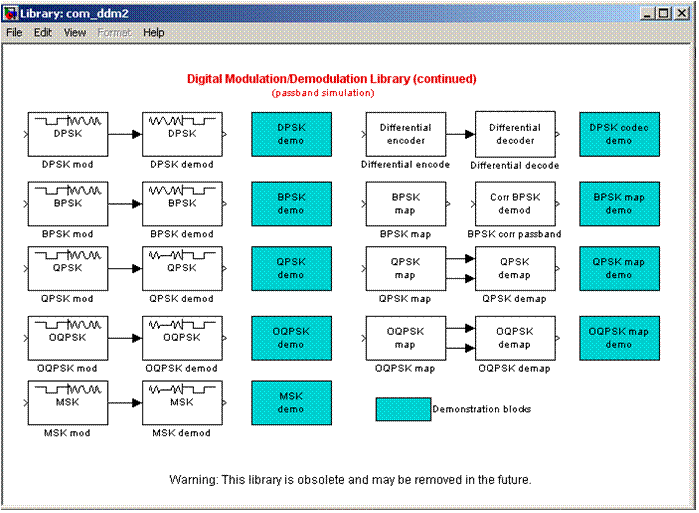
7. На появившейся
схеме найти модулятор QPSK mod, правой кнопкой мыши нажать на нем и “снять маску” с
модулятора: 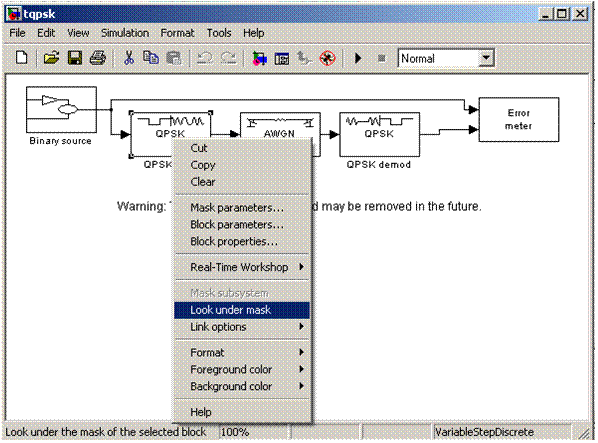
8. Появится
окно со схемой модулятора ФМ-4,надо “снять маску” с двух средних блоков: 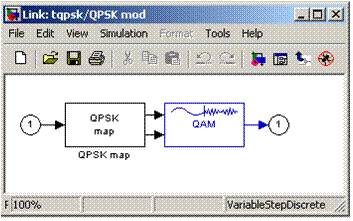
9. Чтобы в
схему добавить осциллограф, надо вызвать Simulink Library Browser. В этой библиотеке выбрать Sinks,
потом найти осциллограф и “перетащить” его в схему: 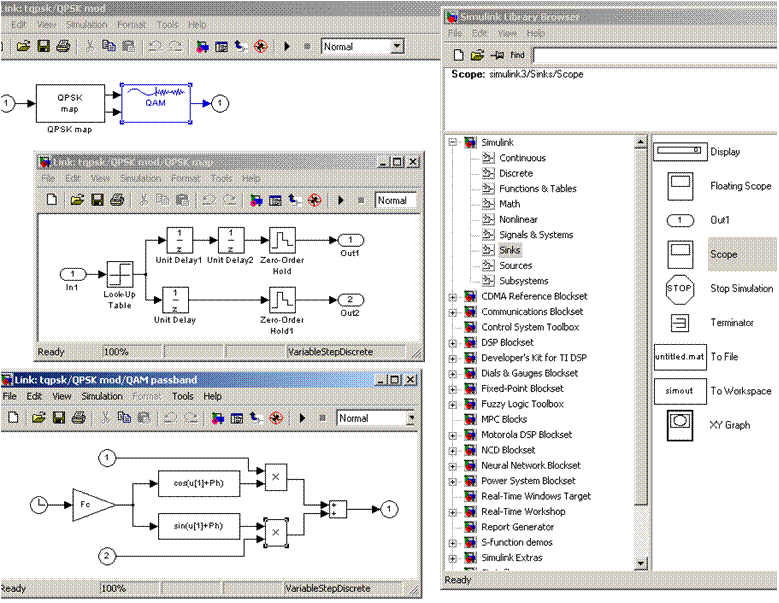
10. Вставить осциллографы в места схемы, где надо проследить изменение сигнала. Посмотреть на сигнал можно двоекратным нажатием на осциллограф.
11. Запустить работу схемы можно нажатием черного треугольника на панели инструментов.
Контрольные вопросы:
1. Что такое квадратурная фазовая модуляция? Рассказать принципы работы.
2. Чем отличается двоичная фазовая модуляция(ФМ-2) от квадратурной фазовой модуляции(ФМ-4)?
3. Что такое сигнальное созвездие? Как его строить?
4. Нарисовать функциональную схему ФМ-4. Рассказать принцип работы каждой части схемы. Показать, как изменяется сигнал после прохождения каждой части схемы.
5. Придумать свой сигнал и промодулировать его.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.