Расчет количественных показателей и определение модели информационного потока, страница 4

L сокращается с 12-ти до 7

4.  Сравним эмпирические частоты n_i и теоретические частоты N_i по критерию Пирсона. Для этого вычислим статистику:

Далее по таблице критических точек распределения для определенного числа степеней свободы k = L – 2 и уровня значимости α найдем значение .

k = 5

α = 0,01

Тогда

Так как    и  меньше , то бессмысленно отвергать гипотезу Пирсона об экспоненциальном распределении.

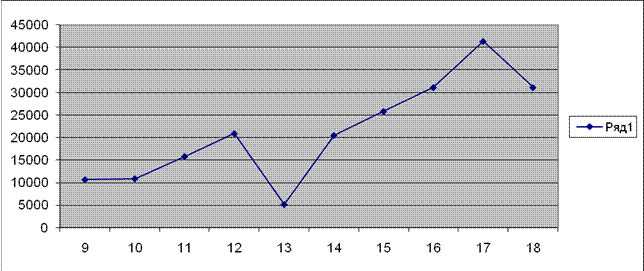
Зависимость от периода

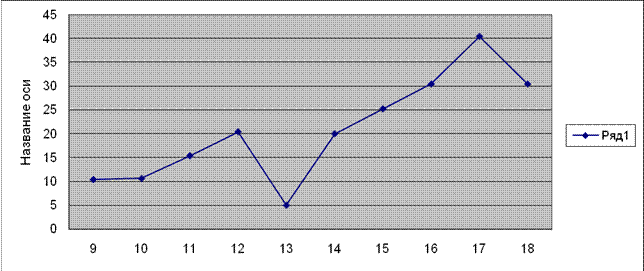
Зависимость S_{j от} периода

Целью проводимого анализа является определение требований к средствам связи пользователя, в адрес которого передается поток сообщений с определенными выше характеристиками. В нашем случае поток пуассоновский, а время передачи сообщения распределено по экспоненциальному закону, следовательно, для расчета можно использовать модель одноканальной системы массового обслуживания  М/М/1.

Расчет для пуассоновского потока и экспоненциального времени обслуживания имеет смысл проводить и в том случае, если экспериментальные данные не согласуются с данными предположениями, так как пуассоновский поток и экспоненциальное время обслуживания являются наиболее «тяжелым» для обслуживания случаем.

В большинстве случаев достаточно сложно рассчитать точные значения необходимых параметров средств связи, например, физической скорости передачи информации по каналу связи, так как необходимо учитывать издержки, вносимые используемыми протоколами, задержки в узлах сети и т.д. Однако соответствующие оценки можно получить исходя из значений эффективной пропускной способности средств связи.

Для системы М/М/1 среднее время передачи сообщений пользователю с учетом времени ожидания в очереди на передачу (которая предполагается бесконечной) рассчитывается по формуле:

,

где λ – интенсивность поступления сообщения, μ – интенсивность обслуживания, определяющаяся эффективной пропускной способностью средств связи С и среднего размера сообщения V:

.

Отношение интенсивности поступления к интенсивности обслуживания называется загрузкой системы  ρ:

.

Для определения С необходимо сформулировать требования к временным характеристикам обслуживания. Требования могут быть, например, следующими:

1.  Необходимо, чтобы среднее время передачи сообщений было не больше некоторого Т_ср.max. Необходимую для заданного Т_ср минимальную эффективность пропускную способность для рассчитанной интенсивности наблюдаемого потока можно рассчитать по формуле:

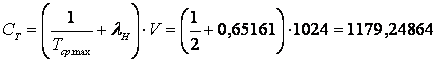
2.  Необходимо, чтобы загрузка ρ была не больше заданной ρ_max. Необходимую для заданного ρ_max минимальную эффективную пропускную способность для рассчитанной по интенсивности наблюдаемого потока можно рассчитать по формуле:

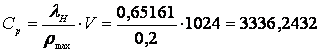
Для выполнения обоих требований одновременно, необходимо обеспечить максимальную из С_Т и С_ρ эффективную пропускную способность.