Расчет количественных показателей и определение модели информационного потока, страница 3

Для проверки гипотезы об экспоненциальном законе распределения длительности промежутков времени необходимо:

1.  Оценим параметр λ. Оценка λ_н определяется через выборочное среднее X_в заданного эмпирического распределения:

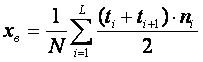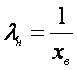,    , 1/с

где L – число интервалов,  и  − границы i-ого интервала, N – общее число наблюдений, определяемое как сумма частот n_i:

 

N = 202

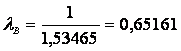  1/с

2.  Определим вероятность P_i попадания случайной величины распределенной по экспоненциальному закону с параметром λ_в в i-ый интервал, заданный границами  и :

3.  Определим теоретические частоты попадания случайной величины, распределенной по экспоненциальному закону с параметром λ_в при общем числе наблюдений N:

Экспортированная таблица из расчетного файла:

Pi	Ni	ni
0,72835	147,12670	162,00000	1,50357
0,19786	39,96772	28,00000	3,58355
0,05375	10,85750	10,00000	0,06772
0,01460	2,94920	2,00000	0,30550
0,00397	0,80194	0,00000	0,80194
0,00142	0,28684	0,00000	0,28684
0,00005	0,01010	0,00000	0,01010
0,00000	0,00000	0,00000
0,00000	0,00000	0,00000
0,00000	0,00000	0,00000
0,00000	0,00000	0,00000
0,00000	0,00000	0,00000