Практикум по курсу "Математические основы теории систем": Учебное пособие (Программа курса, методические указания по изучению курса и контрольные задания)

1. Введение.

1.1. Цель курса

Предметом курса "Математические основы теории систем" является изучение студентами математических методов анализа сложных систем.

1.2. Задачи курса.

Задачи курса "Математические основы теории систем" заключаются в обучении студентов методам анализа сложных систем на основе методов дифференциального исчисления, математического программирования, дискретной математики и теории вероятностей.

2. Общие методические указания по изучению курса.

Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом. Для облегчения этой работы кафедра высшей математики организует чтение лекций и проведение практических занятий. Поэтому процесс изучения курса "Математические основы теории систем" состоит из следующих этапов:

1) проработка лекционного материала;

2) проработка материала практических занятий;

3) самостоятельная работа над учебниками и учебными пособиями;

4) выполнение одной контрольной работы;

5) сдача зачета.

3. Содержание курса.

3.1. Наименование разделов и тем.      

Тема №1. Основные положения системного анализа сложных систем.

Определение понятия системы. Виды связей между элементами системы. Большие и сложные системы. Системный подход к исследованию сложных систем. Эмерджентность сложных систем. Закон синергии. Исследование систем на основе принципа аналогии. Исследование систем на основе метода моделирования. Исследование систем на основе физических моделей. Понятие модели "черного ящика". Исследование систем на основе математических моделей. Виды математических моделей. Исследование систем на основе имитационного моделирования. Кибернетический подход при исследовании сложных систем. Общая

Задача №5. Решить методом множителей Лагранжа задачу нелинейного программирования по вариантам

1. Найти экстремум функции

           при условии .

2. Найти экстремум функции  

           при условии .

3. Найти экстремум функции

           при условии

4. Найти экстремум функции       

           при условии .                                        

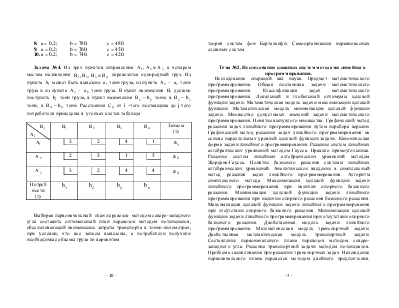
8.   a=  0,2;         b = 780;              c = 480.

9.   a = 0,2;         b = 760;              c = 450.

10. a = 0,2;         b = 740;              c = 420.

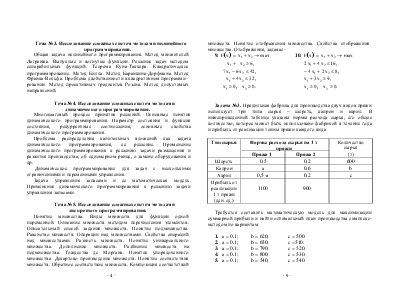
Задача №4. Из трех пунктов отправления  к четырем местам назначения  перевозится однородный груз. Из пункта  может быть вывезено  тонн груза, из пункта  -   тонн груза и из пункта  -   тонн груза. В пункт назначения  должно поступить  тонн груза, в пункт назначения  тонн, в  тонн, в  тонн. Расстояния  от i –того поставщика до j-того потребителя приведены в  уголках клеток таблицы

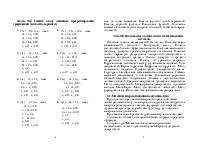
Выбирая первоначальный  план перевозок  методом северо-западного угла составить оптимальный план перевозок методом потенциалов, обеспечивающий наименьшие затраты транспорта в тонно-километрах, при условии, что все запасы вывезены, а потребители получили необходимые объемы груза по вариантам 

теория систем фон Берталанфи. Самоорганизация неравновесных сложных систем.

Тема №2. Исследование сложных систем методами линейного программирования.

Исследование операций как наука. Предмет математического программирования. Общая постановка задачи математического программирования. Классификация задач математического программирования. Локальный и глобальный оптимумы целевой функции задачи. Математическая модель задачи максимизации целевой функции. Математическая модель минимизации целевой функции задачи. Множество допустимых значений задачи математического программирования. Понятие выпуклого множества. Графический метод решения задач линейного программирования путем перебора вершин. Графический метод решения задач линейного программирования на основе параллельных уровней целевой функции задачи. Каноническая форма задачи линейного программирования. Решение систем линейных алгебраических уравнений методом Гаусса. Правило прямоугольника. Решение систем линейных алгебраических уравнений методом Жордана-Гаусса. Понятие базисного решения системы линейных алгебраических уравнений. Аналитическое введение в симплексный метод решения задач линейного программирования. Алгоритм симплексного метода. Максимизация целевой функции задачи линейного программирования при наличии опорного базисного решения. Минимизация целевой функции задачи линейного программирования при наличии опорного решения базисного решения. Максимизация целевой функции задачи линейного программирования при отсутствии опорного базисного решения. Минимизация целевой функции задачи линейного программирования при отсутствии опорного базисного решения. Двойственная модель задачи линейного программирования. Математическая модель транспортной задачи. Двойственная математическая модель транспортной задачи. Составление первоначального плана перевозок методом северо-западного угла. Решение транспортной задачи методом потенциалов. Проблема зацикливания при решении транспортных задач. Нахождение первоначального плана перевозок методом двойного предпочтения. Нахождение первоначального перевозок методом минимальной стоимости.     

Тема №3. Исследование сложных систем методами нелинейного программирования.

Общая задача нелинейного программирования. Метод множителей Лагранжа. Выпуклые и вогнутые функции. Решение задач методом сепарабильных функций. Теорема Куна-Таккера. Квадратическое программирование. Метод Билла. Метод Баранкина-Дорфмана. Метод Франка-Вольфа. Проблема двойственности в квадратичном программи-

ровании. Метод проективных градиентов Розена. Метод допустимых направлений.

Тема №4. Исследование сложных систем методами динамического программирования.

Многошаговый процесс принятия решений. Основные понятия динамического программирования. Параметр состояния и функция состояния, рекуррентные соотношения; основные свойства динамического программирования.

Проблема распределения капитальных вложений как задача динамического программирования, ее решение. Применение динамического программирования к решению задачи размещения и развития производства, об одномерном ранце, о замене оборудования и др.

 Динамическое программирование для задач с несколькими ограничениями и переменными управления.

Задача управления запасами и ее математическая модель. Применение динамического программирования к решению задачи управления запасами.

Тема №5. Исследование сложных систем методами дискретного программирования.             

Понятие множества. Виды множеств для функции одной переменной. Описание множеств методом перечисления элементов. Описательный способ задания множеств. Понятие подмножества. Равенство множеств. Операции над множествами. Свойства операций над множествами. Разность множеств. Понятие универсального множества. Дополнение множеств. Разбиение множеств на подмножества. Тождества де Моргана. Понятие упорядоченного множества. Декартово произведение множеств. Понятие соответствия множеств. Обратное соответствие множеств. Композиция соответствий множеств. Понятие отображения множества. Свойства отображения множества. Отображения, задавае-

9.                  10.       

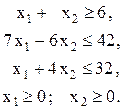
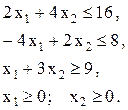
Задача №3. Прядильная фабрика для производства двух видов пряжи использует три типа сырья – шерсть, капрон и акрил. В нижеприведенной таблице указаны нормы расхода сырья, его общее количество, которое может быть использовано фабрикой в течение года и прибыль от реализации тонны пряжи каждого вида

Требуется составить математическую модель для максимизации суммарной прибыли и найти оптимальный план производства симплекс