Практикум по курсу "Дискретная математика": Учебное пособие (Программа курса, методические указания для самостоятельной работы и контрольные задания), страница 3

3. Разностью множеств А и В называется новое множество , которое содержит элементы множества А и не содержит элементы множества В.

На основании приведенного определения можно записать

.                    (1.6)

4. Дополнением множества А называется множество , которое определяется равенством . На основании приведенного определения и определения понятия разности множеств можно записать

.

5. Дополнением множества  называется множество , определяемое равенством

.

Задание №2. Доказать тождество на основе эквивалентных преобразований левой или правой частей равенства

.                             (2.1)

Доказать записанное тождество на основе эквивалентных преобразований означает показать, что левая часть равенства эквивалентна правой или наоборот показать, что правая часть эквивалентна левой.

Для рассмотренной проблемы покажем, что левая часть эквивалентна правой для чего воспользуемся определением операции разности множеств

Далее воспользуемся свойством сочетательности множеств

.

После этого применяем свойство коммутативности (перестановки) множеств и опять свойство сочетательности, после чего получаем

.

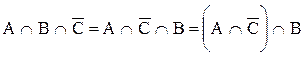После применения определения операции разности множеств окончательно получаем, что левая часть выражения (2.1) принимает вид

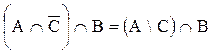.                                 (2.2)

Согласно выражения (2.2) заключаем, что на основе эквивалентных преобразований мы показали, что левая часть исходного равенства (2.1) эквивалентна ее правой части, таким образом, тождество доказано.

Задание 3. На множестве натуральных чисел N заданы отношения

,

 .

Найти композиции отношений , , ,. В ответах привести первые три кортежа последовательности.

1. Композицией бинарных отношений   и   называется новое бинарное отношение при условии, что существуют такие пары  , что если найдется такое значение с, то пары , а пары . На основании приведенного определения композиции бинарных отношений его можно записать на основе описательного способа задания множеств в следующем виде

=

 =

 .

Окончательно можно записать, что

= .

Аналогичным образом можно получить и выражения для остальных трех композиций отношений

2. ,

3. ,

4. .

Задание 4. Методом математической индукции доказать, что число  кратно 9 для всех натуральных .

1. Проверяем исходное утверждение для 

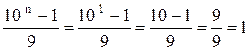.                             (4.1)

Из приведенного выражения (4.1) заключаем, что исходное утверждение выполняется для значения .

2. Выдвигаем гипотезу относительно того, что исходное утверждение выполняется для натурального , т.е. считаем, что число 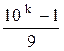является целым.

3. На основании выдвинутой гипотезы покажем справедливость исходного утверждения для значения

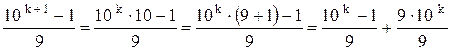.   (4.2)

Из выражения (4.2) заключаем, что первое слагаемое является целым числом согласно выдвинутой гипотезы, а второе слагаемое, равное , является также целым числом.

4. На основании проведенного рассмотрения заключаем, что исходное утверждение выполняется для любого натурального числа .

Задание 5.

Решение задач комбинаторного анализа основывается на определениях основных понятий комбинаторики.

а. Числом перестановок называется число комбинаций, которые можно составить из  элементов, в которых элементы различаются порядком следования. Число  перестановок определяется на основании следующего выражения

.                                                     (5.1)

В выражении (5.1) число  называется - факториал и определяется по формуле

.                               (5.2)

В качестве исключения принимается, что выполняются следующие соотношения

,

.

b. Числом размещений   из элементов по  элементов называется число комбинаций, которые можно составить из  элементов и в которых элементов различаются как составом, так и порядком следования. Число размещений из по элементов без повторения элементов в комбинациях вычисляется по следующей формуле

.

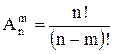c. Числом сочетаний   из элементов по   элементов называется число комбинаций, которые можно составить из  элементов и в которых элементов различаются только составом, а порядок их следования является безразличным. Число сочетаний   из по   элементов без повторения элементов в комбинации вычисляется по следующей формуле

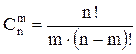.                                     (5.3)

Задача. Решить уравнение

.                                            (5.4)

1. Найдем область определения уравнения на основании определения числа сочетаний элементов, для этого запишем следующую систему неравенств

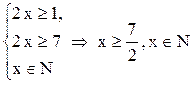.                             (5.5)

2. На основании приведенного определения числа сочетаний по формуле (5.3) уравнение (5.4) можно записать в виде

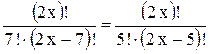.                          (5.6)