2) изучать курс дискретной математики систематически, так как в противном случае материал будет усвоен поверхностно;
3) пользоваться каким-то одним учебником или учебным пособием (или ограниченным числом пособий) из приведенного списка рекомендуемой литературы, чтобы не утрачивалась логическая связь между отдельными вопросами, по крайней мере, внутри какого-то определенного раздела курса.
В процессе изучения дискретной математики студент должен выполнить одну контрольную работу. Контрольная работа позволяет закрепить теоретический материал курса. Решение задач контрольной работы является проверкой степени усвоения студентом теоретического курса, а рецензия преподавателя помогает ему доработать и правильно освоить различные разделы курса дискретной математики. Перед выполнением контрольной работы необходимо внимательно ознакомиться с примерами решения задач по данной контрольной работе, соответствующими уравнениями и формулами, приведенными в методическом пособии.
Прежде чем приступить к решению той или иной задачи, необходимо хорошо понять ее содержание и поставленные вопросы.
Номер варианта контрольной работы необходимо выбирать по последней цифре номера зачетной книжки.
При выполнении контрольной работы необходимо соблюдать следующие правила:
1) указывать на титульном листе наименование дисциплины, вариант контрольной работы, группу, фамилию и инициалы студента;
2) контрольную работу следует выполнять аккуратно, оставляя поля для замечаний преподавателя;
3) задачу своего варианта переписывать полностью;
4) решение задачи и используемые формулы должны сопровождаться пояснениями;
5) в пояснениях к задаче необходимо указывать те основные законы и формулы, на которых базируется решение данной задачи;
6) при получении расчетной формулы для решения конкретной задачи приводить ее вывод;
7) в контрольной работе следует указывать учебники и учебные пособия, которые использовались при решении задач.
Контрольная работа, оформленная без соблюдения указанных правил, а также работа, выполненная не по своему варианту, не засчитывается.
5. Вопросы для самоконтроля и сдачи зачета или экзамена.
1. Определение множества.
2. Способы задания множеств.
3. Объединение множеств.
4. Пересечение множеств.
5. Разность множеств.
6. Свойства операций над множествами
7. Пустое множество и его свойства.
8. Универсальное множество.
9. Дополнение множества.
10. Основные тождества алгебры множеств.
11. Законы де Моргана.
12. Декартово произведение множеств.
13.Бинарные отношения на множестве и их способы задания.
14. Операции над бинарными отношениями.
15. Понятие соответствия множеств.
16. Область определения и область значений соответствия.
17. Обратное соответствие между множествами.
18. Композиция соответствий множеств.
19. Понятие отображения множеств. Свойства отображения множеств.
20. Понятие функции одной переменной.
21. Понятие обратной функции.
22. Композиция функций.
23. Метод математической индукции.
24. Перестановки элементов.
25. Размещения элементов.
26. Сочетания элементов.
6. Методические указания к решению задач контрольной работы.
, 
, 
, 
, 
, 
, если
универсальное множество имеет вид 
, а множества А и В заданы
следующим образом 
,
.
Множество А задано описательным способом, а множества 
и В заданы методом перечисления элементов.
Для удобства оперирования с тремя множествами приведем все множества к одному
способу задания перечислением элементов.
Множество А задано описательным способом таким образом, что элементы множества удовлетворяют квадратному алгебраическому уравнению следующего вида
. (1.1)
Решим квадратное уравнение (1.1), предварительно вычислив его дискриминант
.
(1.2)
Из условия (1.2) следует, что квадратное алгебраическое уравнение (1.1) имеет два различных действительных корня, которые находятся следующим образом
,
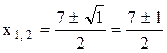таким образом, получаем, что
. (1.3)
Согласно выражения (1.3) заключаем, что множество А методом перечисления элементов можно задать следующим образом
.
1.
Объединением множеств А и В называется новое множество 
,
которое содержит элементы хотя бы одного из множеств А или В.
На основании приведенного определения можно записать
. (1.4)
2. Пересечением
множеств А и В называется новое множество 
,
которое содержит одновременно элементы обоих множеств А и В.
Согласно приведенного определения можно записать
. (1.5)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.