Модель оценки стоимости опционов Блэка–Шоулза

Вопрос 83. Модель оценки стоимости опционов Блэка–Шоулза.

В модели Блэка–Шоулза время движется непрерывно, так как длительность каждого единичного периода устремлена к нулю, т.е модель непрерывной и основывается на том, что число звеньев дерева бесконечно велико, а длина каждого интервала соответственно бесконечно мала.

Модель Блэка–Шоулза, являясь частным случаем биномиальной модели, основывается на следующих предпосылках.

1. Цена акции меняется постоянно и временные интервалы в модели очень короткие.

2. Изменение цены акции рассматривается как случайный процесс. Теоретически при очень коротких временных интервалах цены акции во времени изменяются очень слабо и изменение цен может быть описано в таком случае непрерывным нормальным распределением. Нормальное распределение, однако, допускает, как известно, отрицательные значения переменной величины, что не соответствует случаю акции, цена которой не может опуститься ниже нуля (ответственность акционеров ограничена). Более того, нормальное распределение предполагает равную вероятность подъема и снижения цены, хотя в реальной действительности инфляция приводит к бóльшему изменению цены в сторону повышения. С учетом этого в рассматриваемой модели используется распределение натурального логарифма относительных цен на акции. Кривая логнормального распределения представлена на рис. 1.

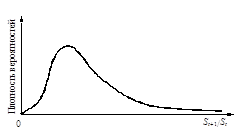Рис. 1. График функции логнормального распределения

3. Отсутствуют дивидендные выплаты.

4. Опцион может быть исполнен только в фиксированный момент времени (европейской опцион).

5. Нейтральность инвестора по отношению к риску.

6. Отсутствуют трансакционные издержки и несовершенства рынка.

7. Факторами, определяющими стоимость опциона, являются:

а) текущая цена акции (S0);

б) цена исполнения опциона (Е);

в) срок действия опциона (Т);

г) безрисковая доходность, соответствующая сроку действия опциона ();

д) дисперсия натурального логарифма цены акции (s²); в качестве случайной величины (переменной) для расчета дисперсии берется значение ln(S_t+1/S_t).

Для понимания модели Блэка–Шоулза на интуитивном уровне рассмотрим функционал: S₀ – . В этом выражении S₀ представляет курсовую стоимость базисной акции на момент оценки стоимости опциона колл, выписанного на нее. Соответственно  есть приведенная величина будущих затрат по покупке акции. Поэтому величина S₀ –  может быть рассмотрена как некоторый аналог приведенной величины будущих платежей по исполнению опциона. А это и есть его цена на начало периода.

Однако, поскольку полной уверенности в исполнении опциона на самом деле нет, то необходимо ввести некоторые уточняющие весовые коэффициенты N(d1) и N(d2), связанные с вероятностью исполнения опциона и прогнозируемым темпом роста цены базисной акции.

Формулы Блэка–Шоулза для расчета стоимости опциона колл (Vc) и опциона пут (Vp) с учетом вышесказанного будут иметь следующий вид:

,   ,

где S₀ – текущий курс базисной акции; Е – цена исполнения опциона; е – основание натурального логарифма (2,71828);  – безрисковая процентная ставка, начисляемая по формуле сложных процентов; Т – время, остающееся до срока истечения опциона, рассчитываемое как доля года (количество дней до даты истечения, деленное на 365);  – приведенная (текущая) оценка цены исполнения при непрерывном дисконтировании; N(d₁) и N(d₂) – значения накопленной вероятности соответственно по d₁ и d₂ для стандартизированного нормального распределения.

Стандартизированная (или нормированная) переменная рассчитывается по формуле:

, где m – математическое ожидание переменной х.Если случайная переменная х нормально распределена, то стандартизированная переменная d будет распределена также нормально с математическим ожиданием, равным нулю и средним квадратическим отклонением, равным единице, рис. 2.

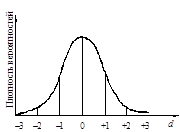Рис. 2. Стандартизированная функция плотности вероятностей нормальной кривой

Поскольку нормальное распределение – это распределение вероятностей, то площадь под кривой должна быть равна единице.

Отсюда следует, что, например, N(0) = 0,5; N(+¥) = 1,0; N(–¥) = 0.

Учитывая значимость и широкое использование стандартизированного нормального распределения, таблицы накопленной вероятности N(d) приводятся в любом солидном учебнике по статистике. В них приводятся площади под стандартной кривой нормального распределения – так называемого стандартизованного нормального распределения. Обычно в таблице при помощи диаграммы указывается, площадь каких сегментов приводится.

Предположим, например, мы знаем, что ежедневная доходность конкретной ценной бумаги нормально распределена с математическим ожиданием, равным 0,5%, и средним квадратическим отклонением 0,1%, и мы хотим определить вероятность того, что ежедневная доходность будет больше 0,525%.

Последовательность расчетов здесь может быть следующей.

1. Определение нормированной величины

2. По таблице N(d) определение площади под кривой между d = 0 и d = 0,25, которая равна 0,0987.

3. Определение вероятности того, что

d < 0,25 : 0,25 + 0,0987 = 0,5987.

Соответственно вероятность того, что d > 0,25 (или доходность выше 0,525%) составит 0,4013, или 40,13% (1 – 0,5987 = = 0,4013).

Кстати, площадь любого вертикального сегмента под кривой N(D) представляет вероятность того, что нормально распределенная случайная величина примет значение на интервале, ограниченным данным сегментом.

В свою очередь параметры d₁ и d₂ в модели Блэка-Шоцзла могут быть рассчитаны по формулам: