Изучение зависимости сопротивления проводников, страница 2

где j – плотность электрического тока; – удельная электропроводность проводника, равная обратной величине удельного сопротивления ; Е – напряжённость электрического поля в проводнике.

            В классической электронной теории полагается, что

где m, v, e – соответственно масса и средняя скорость и заряд электрона; n – концентрация свободных электронов; – длина свободного пробега электронов, которая по порядку величины соответствует расстоянию между узлами кристаллической решётки.

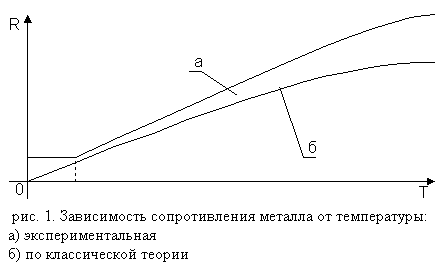            В приведенном уравнении только скорость зависит от температуры. По классической теории электропроводности эта скорость, как и для молекул идеального газа, пропорционально корню абсолютной температуры. Следовательно, сопротивление металлов, как и скорость, должно быть пропорционально корню из температуры (рис. 1). Этот вывод из классической теории противоречит экспериментальной зависимости сопротивления металлов, которая в широком диапазоне температур является линейной:

где R и R₀ – сопротивления металлов при температуре Т и при 0°С соответственно.

            Сопротивления многих металлов (Al, Zn, Pb и др.) и их сплавов при очень низких температурах (0,14 + 20К) скачкообразно уменьшается до 0 (на рис. 1 обозначено показано линией). Это явление называют сверхпроводимостью. Классическая электронная теория электропроводимости металлов встретилась с рядом затруднений, преодолеть которые не смогла:

            1) Вывод теории температурной зависимости сопротивления металла противоречит экспериментальным данным.