Задания на контрольную работу № 3 по дисциплине "Математика". Методические указания по выполнению контрольных работ

выполнении контрольных работ необходимо придерживаться указанных ниже правил:

1.  Каждая контрольная должна быть выполнена в отдельной тетради в клетку. На обложке тетради приводятся данные по образцу:

                           ФГОУ ВПО

  КамчатГТУ

                         Кафедра « Высшая математика»

                                   Математика.

                          Контрольная работа №

                                 Вариант №

Выполнил                                                  Проверил

Студент  гр.                                        доцент    каф. ВМ

  Ф.И.О.                                                                  Суворова Н.В

 Шифр

2.Номер варианта определяется  так: возьмите две последних цифры шифра вашей зачетной книжки из полученного числа отнимите  , где, разность определит номер вашего варианта. Например: если 20; 40; 60;80, то 20 вариант

Две последние цифры		Номер варианта
12		12
24		4
36		16
48		8
50		10
67		7
75		15
89		9
99		19

3.Решение каждой задачи начинается с записи ее условия без сокращений и замены ее содержания. Записи условия и решения вести с соблюдением полей, на которых при проверке преподавателем, при необходимости указываются замечания.

 4.Решения задач должны быть достаточно  подробными. При необходимости следует делать соответствующие ссылки с указанием формул, теорем, которые используются при решении. Все вычисления необходимо выполнять полностью.

5.Контрольные работы, содержащие задачи не своего варианта, не зачитываются.

6.Решения задач можно располагать в любом порядке, сохраняя номера задач.

7.Контрольные работы должны выполняться самостоятельно, при ее защите  студент должен уметь дать устные пояснения к решению задач (по требованию преподавателя).

8.В прорецензированной решенной работе студент должен исправить отмеченные ошибки и учесть рекомендации. Зачтенные контрольные работы предъявляются студентам  на зачете и при сдаче экзамена.

Для  курсантов  очной формы обучения вариант выполнения  индивидуальных заданий определяет преподаватель.

Контрольная работа№3

Задание №1. Дано векторное поле . Построить поля:

а)  

б)

в)

Вар.		Вар.
1		11
2		12
3		13
4		14
5		15
6		16
7		17
8		18
9		19
10		20

Задание №2. Доказать, что данное векторное поле  является потенциальным и найти его потенциал.

Вар.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

Задание №3.

Тело массы  подвешено на спиральной пружине жесткости  и совершает колебания в вязкой среде с коэффициентом сопротивления . На верхний конец пружины действует вынуждающая сила, изменяющаяся по закону  (для вар. 1-10),  (для вар. 11-20).

Найти закон движения тела, считая, что в начальный момент времени оно находилось в покое в положении равновесия.

При решении задачи в вычислениях производить округление до сотых

Задание № 4.  Струна, закрепленная на концах, имеет в начальный момент форму . Методом Фурье определить смещение точек струны от оси абсцисс, если начальные скорости задаются функцией

Вар.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

Задание № 5.Методом Фурье решить уравнение теплопроводности для однородного стержня единичной длины, излучающего с боковой поверхности:

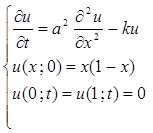
Вар.	а	k	Вар.	а	k
1	1	2	11	3	2
2	4	3	12	1	1
3	3	1	13	1	5
4	2	4	14	4	1
5	2	5	15	2	2
6	3	4	16	3	3
7	2	5	17	2	1
8	4	2	18	4	2
9	5	1	19	5	5
10	1	3	20	1	4

Задание№1. Дано векторное поле

.

Построить поля:

а)  

б)

в)

Решение: Оператор Гамильтона

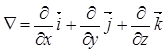
а) Умножая скалярно набла-оператор на данное векторное поле, получаем скалярное поле

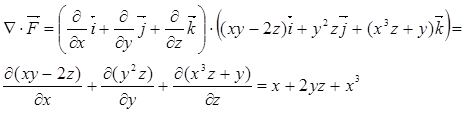
Применяя набла-оператор второй раз, получаем векторное поле :

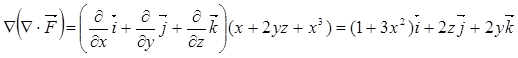
б) Умножая векторно набла-оператор на данное векторное поле, получим новое векторное поле :

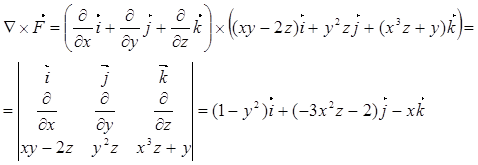
Скалярно умножим оператор Гамильтона на полученное векторное поле. В результате получим скалярное поле :

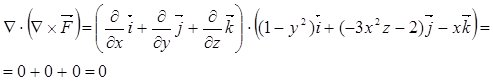
в) Из предыдущего пункта

Второй раз векторно применим оператор Гамильтона, получая векторное поле:

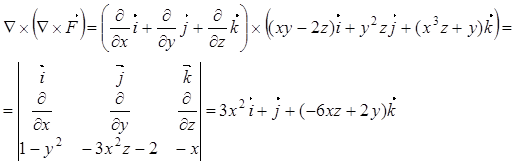
Задание №2. Доказать, что данное векторное поле

является потенциальным и найти его потенциал.

Решение: Векторное поле является потенциальным, если

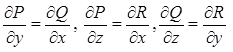
Проверим эти условия:

.

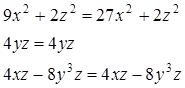Следовательно, данное векторное поле потенциальное.

Его потенциал может быть найден по формуле :

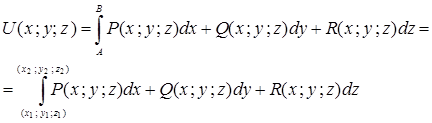
Пусть точка  -  начало координат, точка  - произвольная точка с координатами . Поскольку поле потенциально, криволинейный интеграл не зависит от пути интегрирования. Выберем в качестве пути интегрирования ломаную .

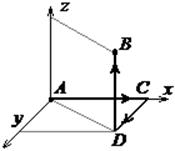
В силу аддитивности криволинейного интеграла второго рода, имеем следующее:

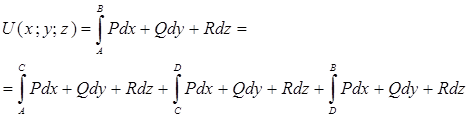
Т.к. отрезки  параллельны координатным осям , получаем :

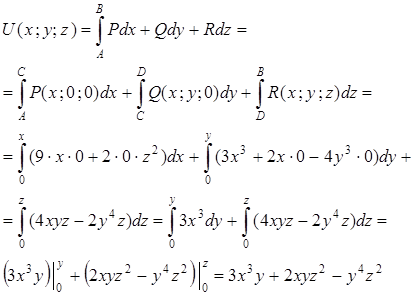
Задание№3.Разложить векторное поле  на сумму потенциального и соленоидального полей.

Решение: Используя :

,

где  - потенциальное поле, а  - соленоидальное поле, причем  - решение уравнения