Задания к контрольной работе № 1 по дисциплине "Математика". Образцы решения задач. Вопросы для итогового контроля знаний

Вычислить: а), б) – неопределенный интеграл, в) – определенный интеграл

№	Задания
6.1.	а)	б)	в)
6.2.	а)	б)	в)
6.3.	а)	б)	в)
6.4.	а)	б)	в)
6.5.	а)	б)	в)
6.6.	а)	б)	в)
6.7.	а)	б)	в)
6.8.	а)	б)	в)
6.9.	а)	б)	в)
6.10.	а)	б)	в)

Задание №7.

Найти частные производные первого и второго порядка.

№	Задание	№	Задание
7.1.		7.6.
7.2.		7.7.
7.3.		7.8.
7.4.		7.9.
7.5.		7.10.

Задание №8.

 Найти общее решение дифференциального уравнения.

№	Задания
8.1.	а)	б)	в)
8.2.	а)	б)	в)
8.3.	а)	б)	в)
8.4.	а)	б)	в)
8.5.	а)	б)	в)
8.6.	а)	б)	в)
8.7.	а)	б)	в)
8.8.	а)	б)	в)
8.9.	а)	б)	в)
8.10.	а)	б)	в) о

Образцы решения задач.  

Задача №1. Решить систему линейных уравнений методом Крамера, матричным методом и методом Гаусса.

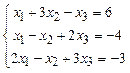
Решение.

1.) Метод Крамера.

Найдем определитель коэффициентов системы:

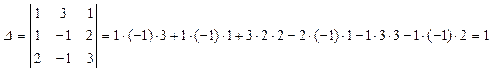
Вычислим ,  и :

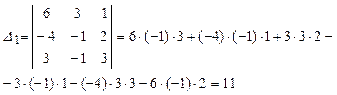
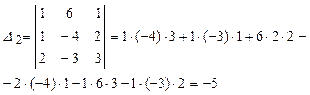
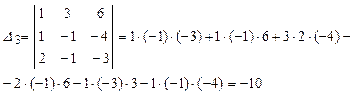
Следовательно:

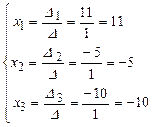
Проверка. Подставляя полученные значения корней в уравнения системы, получаем верные равенства:

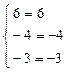
2). Матричный метод.

Пусть матрица  - матрица коэффициентов системы,  - матрица-столбец переменных,  - матрица-столбец свободных членов.

, , .

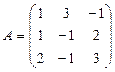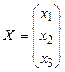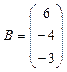решение системы будем искать по формуле . Обратную матрицу найдем по формул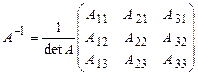е , где  - алгебраическое дополнение элемента , а  - минор элемента . Поскольку . Вычислим алгебраические дополнения:

, , ,

, , ,

, , .

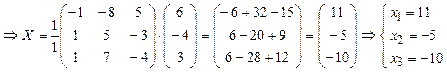
3). Метод Гаусса.

Составим расширенную матрицу системы преобразуем с помощью элементарных преобразований:

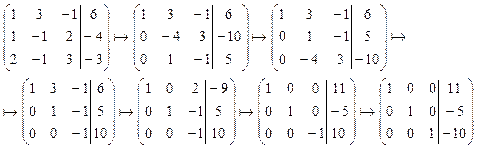
В результате слева получена единичная матрица, а справа - значения соответствующих переменных.

Ответ: .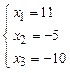

Задание №2. Исследовать и решить систему линейных уравнений.

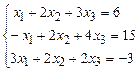
Решение.

Исследуем эту систему по теореме Кронекера-Капелли. Найдем ранг основной матр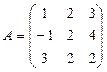ицы системы  и ранг расширенной матрицы системы .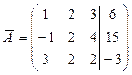

.

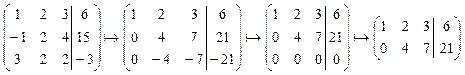система совместна. А т.к.  (где  - число неизвестных в системе), то система неопределенна и имеет бесконечное множество решений. Выберем переменные  и  в качестве базисных и выразим их через свободную переменную .

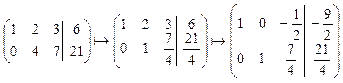
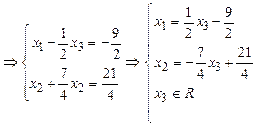 - общее решение.

Фиксируя свободную переменную, можно получить частные решения: , .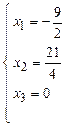

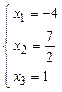Задача №3. Даны координаты вершин : , , Найти:

1. Длину стороны

2. Уравнения сторон  и

3. Уравнение высоты , опущенной из вершины

4. Уравнение медианы  и координаты точки  - точки пересечения этой медианы с высотой

Решение.

1). Расстояние между точками  и  определяется по формуле

.

Ответ:

2). Уравнение прямой, проходящей через точки  и  имеет вид:

.

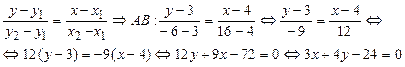Последнее уравнение может быть представлено в виде уравнения с угловым коэффициентом: .

.

Ответ: , , , .

3). Уравнение прямой, проходящей через данную точку в заданном направлении имеет вид: . Высота . Чтобы найти угловой коэффициент высоты , воспользуемся условием перпендикулярности прямых:

.

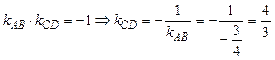Подставляя в формулу координаты точки  и найденный угловой коэффициент высоты, получим ее уравнение:

.

Ответ:

4). Чтобы найти уравнение медианы , определим сначала координаты точки  - середины стороны . Формулы для нахождения координат середины отрезка:

.

Подставляя координаты найденной точки  и точки  в уравнение , получаем искомое уравнение медианы . Чтобы найти координаты точки пересечения высоты  и медианы , решим систему  уравнений:

Ответ: , .

Задача №4. Вычислить пределы функций, не пользуясь правилом Лопиталя.

Решение.

а). 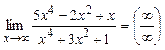. Применим метод деления числителя и знаменателя на  в наивысшей степени:

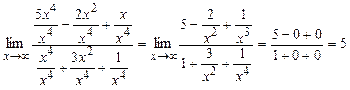
б). 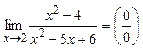. Применим метод разложения числителя и знаменателя на множители:

в). 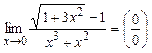. Применим метод домножения числителя и знаменателя на сопряженное выражение:

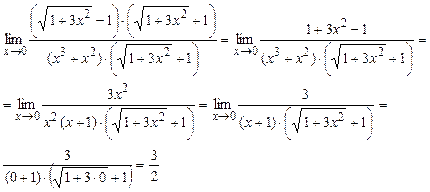
г). . Применим тригонометрическую формулу  и первый замечательный предел .

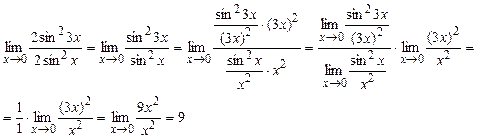
д). В процессе решения воспользуемся вторым замечательным пределом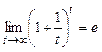

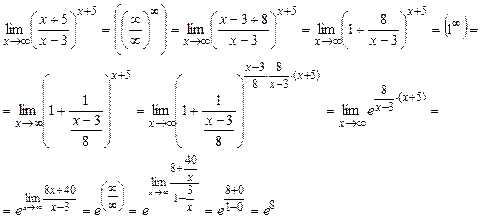
Задача №5. Найти производную функции.

Решение.

а). . Воспользуемся формулой производной произведения двух функций .

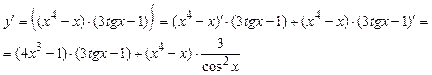
б). 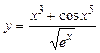. Воспользуемся формулой производной частного двух функций  и формулой производной сложной функции .

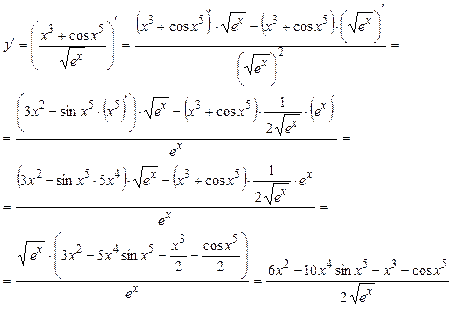
Задача №6. Исследовать на экстремум функцию одного аргумента.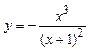

Решение. Находим первую производную функции по формуле  и используем необходимое условие экстремума  для определения точек «подозрительных» на экстремум:

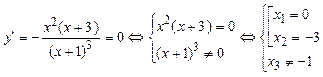
Исследуем полученные точки и поведение функции, определяя знак первой производной слева и справа от каждой точки. Для наглядности результат представим в виде таблицы.

В первой строке указаны интервалы, на которые область определения функции разбивается точками  и сами эти точки. Во второй строке указаны знаки производной в интервалах монотонности. В третьей строке производится заключение о поведении функции в точках и на интервалах. Т.о. из таблицы следует, что  - точка минимума, . Точка  не является точкой экстремума, поскольку в ней не определена функция. Точка  также не является точкой экстремума, т.к. при переходе через нее первая производная сохраняет знак.

Ответ:

Задание №7. Вычислить: а), б) – неопределенный интеграл, в) – определенный интеграл

Решение.

а). . Воспользуемся методом замены переменной.

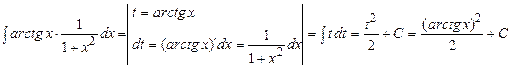б). . Воспользуемся методом интегрирования по частям , применяя эту формулу дважды