Доходность облигаций. Модель Миллера. Структура капитала и индивидуальные налоги инвесторов

1. Доходность облигаций

Расчёт доходности, или инвестиционной нормы, кот.облигация будет обеспечивать, когда будет куплена за данную цену помогает инвестору определить какая из нескольких облигаций обеспечит ему наилушую инвестицию..

В самом общем случае под доходностью любой инвестиции понимается процентная ставка r, позволяющая уровнять привед.стоим-ть денеж.потоков конкурентной инвестиции с ценой инвестиции.

1.1 для бескупонных облигаций.

 Доходность бескупонной облигации – это годовая ставка процента, получаемая инвестором, купившим и владеющим данной облигацией до момента её погашения.

1.2 для купонной облигации

Различают тек.доходность и внутреннюю ставку дохода, или доходность к погашению.

Тек.доходность находится по формуле:

, где r_T – тек.доходность, С- купонный доход по облиг., Р – тек.цена облигации

Тек.доходность учитывает только купонные выплаты, все остальные источники дохода (напр, прирост капитала) не берутся в расчёт. Данный показатель применяется в случаях когда до погашения облигации остаётся немного времени, и цена обл.будет вряд ли испытывать существ.колебания.

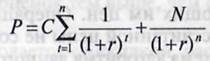Внутренняя доходность Учитывается не только купонный доход, цена облигации, но и период времени, оставшийся до погашения.

Данное уравнение не решается в конечном виде. Можно воспользоваться методом подстановки в формулу цены облигации различных значений внутренней доходности с расчётом сопутствующих им цен. Операцию повторяют до тех пор, пока значение рассчитанной цены не совпадает с заданной ценой облигацией. Алгоритм: 1. задание  исходного уровня доходн.2. определение расчётного уровня цены облигации 3. проверка: расчётн.значение сопоставляется рыночной цене. Если наблюдается равенство – окончание расчёта, если – нет – 4. Если Ррасч.>рыночн.Р, то увеличение рын.Р. Если нет, то уменьшение.

Традиционно используемая формула расчёта приблизительного уровня доходности облигации:

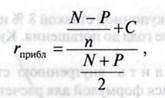,где N – номинальная стоим-ть, Р-цена облигации, т-кол-во лет до погашения, С-купонный доход, числитель – средний годовой доход, знаменатель – средняя стоимость облигации.

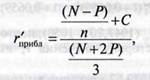В ряде случаев лучшее приближение даёт формула Родригеса:

Используется при купон.ставки<50%  

Если облигация продаётся со скидкой, рассматриваемые формулы дают заниженное значение доходности облигации, если с премией, то завышенное.

Погрешность расчётов тем выше, чем больше лет остаётся до погашения. Процедура повторных расчётов может быть ускорена, если имеется график зависимости привед.стоимости облигации от уровня её внутр.доходности. Также может быть использована формула линейной интерполяции:  

r₁, r₂ – значения соотв.заниженного и завышенного уровней ориентировочной доходности облигаций, P1,P2 – расчётные рыночные цены облигации, соотв.уровням доходности r₁ и r_2; Р – фактическая цена облигации.

Доходность к погашению позволяет оценить не только тек.доход, но и размер прибыли или убытка, ожидающих капитал инвестора при владении облигацией до её погашения. Также учитывает временные параметра ден.потоков. Соотношения основных параметров указаны в табл.справа

2. Модель Миллера. Структура капитала и индивидуальные налоги инвесторов.

В 1997 Мертон Миллер представил модель, демонстрирующую влияние левериджа на стоимость фирмы с учётом как корпоративных, так и личных налогов. Tc – ставка корпоративного налога на прибыль,Ta – ставка налога на доходы индивидуального инвестора от владения акциями корпорации, Td – ставка налога на процентные доходы о представления инвестором – физ.лицом кредитов другим инвесторам и компаниям. С учётом персональных налогов и тех же допущениях, что были сделаны для моделей Модильяни-Миллера (т.е. функц.в идеальной среде), стоим-ть финансово независимой фирмы определяется как: Vu = EBIT (1-Tc)(1-Ta)/k_u , где числитель показывает, какая часть операционной прибыли рассматриваемой фирмы остаётся в распоряжении инвесторов после того, как фирма выплатит налоги на свою прибыль, а её акционеры затем уплатят индив.налоги на доходы от владения акциями. Индивид.налоги снижают общую оценку финансово независимой фирмы.

Оценка финансово зависимой компании: 1. определяем денежные потоки компании CFt = NCF акционеров+NCF кредиторов= (EBIT-1)(1-Tc)(1-Ta)+I*(1-Td), где I- ежегодные процентные платежи по долгу. 2. Преобразование формулы CFt = [EBIT(1-Tc)(1-Ts)]-[I(1-Tc)(1-Ts)]+[I(1-Td)]. Первый член уравнения соотв-т CF для финанс. независимой фирмы. 2-ой и 3-ий члены соотв-т денеж.потокам, связанным с заёмным финансированием. Приведённые стоимости дисконтируются по безрисковой номинальной ставке по долгу k_d .3. Преобразование

V_L = EBIT (1-Tc)(1-Ts)/k_s  - I (1-To)(1-Ts)/k_d + (1-Td)/k_d

V_{L =} Vu + (1-Td)/k_d  *{1 – (1-Tc)(1-Ts)/(1-Td)}, где (1-Td)/k_d равен рыночной стоим-ти долга D.

V_{L =} Vu + D  *{1 – (1-Tc)(1-Ts)/(1-Td)}