Составление уравнений переменных состояния цепи и их численное решение в среде MathCAD

Министерство образования и науки Российской Федерации

   НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ

УНИВЕРСИТЕТ

ФАКУЛЬТЕТ РАДИОТЕХНИКИ И ЭЛЕКТРОНИКИ

КАФЕДРА ОБЩЕЙ ЭЛЕКТРОТЕХНИКИ

Лабораторная работа № 17

"Компьютерный анализ переходных процессов"

    Факультет:  РЭФ

    Группа:  РТВ14-91

    Студент:  Артюшенко В.В.

    Преподаватель:  Давыденко О.Б.

                                                    Новосибирск,  2011

Цель работы

Освоить методику составления уравнений переменных состояния цепи и их численного решения в среде MathCAD.

Рабочее задание

1.  Для полученного индивидуального задания составить, в общем случае, два уравнения: одно – основное – для определения переменной состояния цепи (тока катушки или напряжения конденсатора) и второе (при необходимости) – для искомого тока или напряжения элемента цепи.

2.  Записать выражение импульса задающего напряжения или тока, определенного своим графиком.

3.  Сделать заготовку лабораторной работы, содержащую исходные данные для ее выполнения на компьютере (записать стартовое значение переменной состояния цепи, дифференциальное уравнение в нормальной форме для переменной состояния цепи и при необходимости алгебраическое выражение искомого напряжения или тока).

4.  Открыть окно MathCAD на экране компьютера и создать рабочий документ.

5.  Пользуясь методическими указаниями и примером расчета ввести все необходимые значения и формулы в рабочий документ MathCAD, сохраняя его время от времени.

6.  Получить таблицу значений искомого напряжения или тока элемента цепи. Построить совмещенные графики заданного импульса напряжения или тока и искомой величины.

Исходные данные:

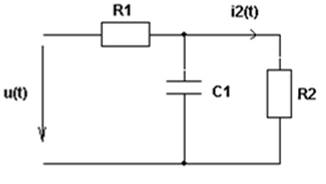
       Параметры элементов:

;

               ;

               ;

                       Рис. 1. Заданная схема

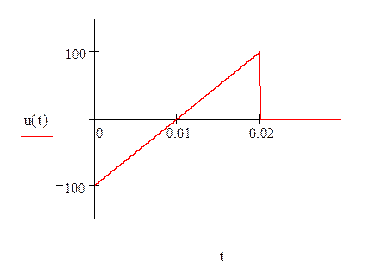
Рис. 2. График входного воздействия

                 1. Получим уравнения для определения переменной состояния цепи . Для этого               составим уравнения по законам Киргхофа для заданной цепи:

                   

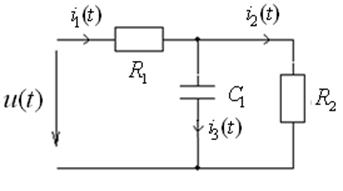
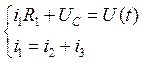
         Ток через конденсатор согласно компонентному уравнению конденсатора выражается через напряжение на конденсаторе следующим образом:

;

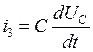         Ток через резистор  равен:

;

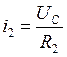         Таким образом, система уравнений приобретает вид:

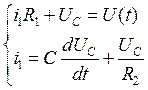
          Выразим ток  из первого уравнения системы и подставим во второе:

;

;

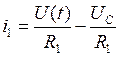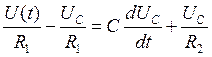           В результате преобразования получаем:

,

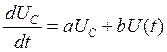           где ,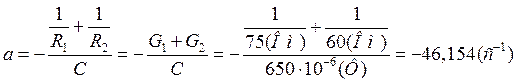

                  ;

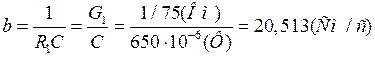            Искомый ток  можно выразить через напряжение на конденсаторе следующим образом:

;

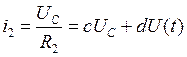            где , ;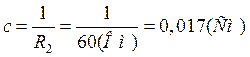

                   2. Найдем постоянную времени цепи:

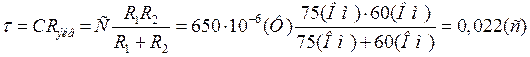
                   3. Запишем аналитическое выражение для импульса задающего напряжения:

:

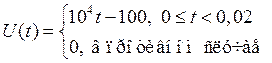                    4. Найдем численное решение уравнения переменной состояния цепи с помощью функции rkfixed математическогоо пакета MathCAD, реализующей метод Рунге-Кутта с фиксированным шагом.

      Текст программы для MathCAD с пояснениями прведен ниже:

       Ввод исходных данных:

                                      

       Время импульса . Будем исследовать переходный процесс в течение времени импульса плюс .

       Ввод выражения для задающего напряжения:

      

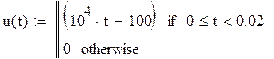
       Стартовое значение переменной состояния цепи :

         

       Выражение ее первой производной:

        

       Выражение значений переменной состояния в тысяче равнооотстоящих точках (1000) интервала времени  с:

      

        Номера точек разбиения интервала времени пробегают значения от0 до числа строк без 1 матрицы Z:

      

        Элементам вектора  присваиваются значения элементов первого столбца матрицы Z:

       

        Элементам вектора  присваиваются значения элементов второго столбца матрицы Z:

        

        Выражение искомой зависимой переменной цепи – тока  резистора  есть линейная функция переменной состояния цепи  и задающего напряжения  и в протоколе       MathCAD выглядит так:

        

        Результат численного решения этой задачи представлен графиком:

   Вывод: математический пакет MathCAD позволяет относительно просто находить численные решения уравнений переменных состояния цепи посредством нескольких алгоритмов (методов), один из которых был использован в данной работе. Точность решения можно изменять в процессе вычислений.