Анализ гармонического процесса в отрезке радиотехнического кабеля генератора мощностью 60 Вт и частотой 1071,4 МГц

Нагруженный отрезок регулярной линии длиной l заменяю эквивалентным         

        сосредоточенным пассивным двухполюсником (рис. 6), значение

        сопротивления которого вычисляют по формуле в тригонометрических

            функциях (3.2.1)  при y=l :

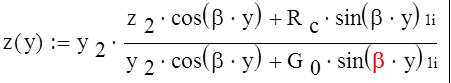                                    ,                                                                                                                                                     (3.2.1)

                 где   y₂- проводимость нагрузки (См),

                           z₂- сопротивление нагрузки (Ом),

                           R_c- волновое сопротивление (Ом),

                           G₀- волновая проводимость(См).

        3.3. Полагая начальную фазу U₀(t) равной нулю, нахожу граничные

                  комплексные значения напряжения и тока в начале отрезка линии:

                              

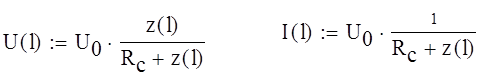
                     где   U₀=134.16 В

              По формуле (3.2.1) нахожу сопротивление z(l) пассивного двухполюсника:

                                                  z(l)=19.4+11.757i  Ом

              Из формул (3.3.1) определяю граничные комплексные значения  напряжения  

              и тока в начале отрезка линии:

                                U(l)=29.2+13.07i В          I(l)=1.39-0.174i А

               Модули величин U(l) и I(l):

            По формулам (3.1.5) и (3.1.6) определяю постоянные интегрирования

            напряжения U_2n и тока I_2n :

U_2n=67.09 В       I_2n=0.89 А

                   Таким образом, распределение действующих значений напряжения и тока

                    вдоль нагруженного отрезка линии без потерь имеют вид ( согласно             

                    формулам (3.1.3) и (3.1.4):

                                        

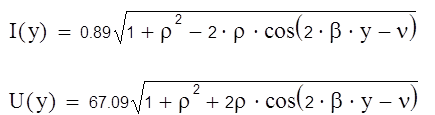
3.4. Графики распределения действующих значений напряжения и тока

y	0	0.03	0.05	0.08	0.1	0.13	0.15	0.18	0.2	0.23
U(y)	77.5	32.4	79.5	105.5	75.9	33.6	80.9	105.1	74.4	31.9
I(y)	1.04	1.4	1.04	0.44	1.06	1.4	0.9	0.46	1.18	1.4

                          

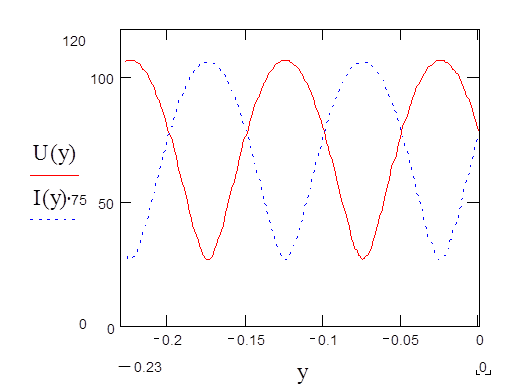
                                     Распределение действующих значений напряжения        

                                            Распределение действующих значений тока

             Рис.7  График распределения действующих значений напряжения и тока

                         вдоль нагруженного отрезка линии без потерь.

4. Расчет распределений вещественной и мнимых частей сопротивления

или проводимости.

                 Согласование осуществляется последовательным шлейфом, поэтому

                 удобнее рассчитать распределения вещественной и мнимой частей 

                 сопротивления.

                Распределения вещественной и мнимой частей сопротивления можно

                получить из формул (4.1) и (4.2):

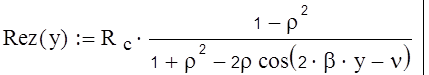                                                                             (4.1)

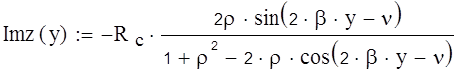                                                       (4.2)

y	0	0.03	0.05	0.08	0.1	0.13	0.15	0.18	0.2	0.23
Rez(y)	35.05	19.45	36.9	199.4	33.7	19.6	38.4	183.9	32.5	19.6
Imz(y)	-65.0	12.2	68.4	-133	-62.5	13.8	71.1	-137	-60	11.7

                                       

                         

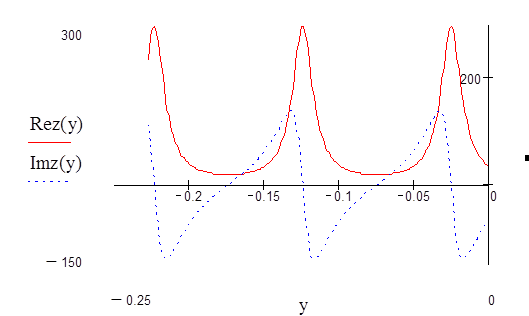
                                       Распределение вещественной части сопротивления

                                               Распределение мнимой части сопротивления

Рис.8 График распределения вещественной и мнимой частей сопротивления.

5. Расчет значений активных мощностей.

                 Активная мощность P(y) – среднее значение мощности за период T=1/f_г

                 в произвольном сечении отрезка линии с координатой y(0≤y≤l); 

                 определяется формулой:

                                                         P(y)=Re[U(y)I(y)]             [Вт]                                                         (5.1)

              С учетом линейной взаимосвязи U(y) и I(y)

U(y)=z(y)I(y)             I(y)=y(y)U(y)     ,

              имеем                 

                                               P(y)=I²(y)Rez(y)=U²(y)Rey(y)                  (5.2)

               Значения активных мощностей в начале P(l) и в конце отрезка линии без

               потерь должны совпадать (окажутся меньше значения мощности 

               генератора P_г).

               По формуле (5.2) рассчитываю значения активной мощности                

                           - в начале линии (y=l)     P(l)=38.234  Вт  ;

                           - в конце линии (y=0)      P(0)=38.234  Вт.

6. Определение значений параметров элементов согласующих устройств

и распределений U(y) и I(y).

               При комплексной нагрузке   z=35-j65 Ом   беру согласующее устройство в

виде короткозамкнутого шлейфа с волновым сопротивлением R_c , который

присоединяется в таком сечении l₁ отрезка линии, в котором вещественная 

часть сопротивления в сторону нагрузки z(l₁)  равна волновому сопротивле-

нию:

                       Rez(l₁)=R_c     -   первое условие согласования.

               Шлейф длиной l₂ , включаемый в сечение l₁, компенсирует мнимую

составляющую сопротивления несогласованного участка линии:

                         Im[z(l₁)+z(l₂)]=0   -  второе условие согласования.

              Значения l₁ и l₂ нахожу из следующих формул при n=1 и k=1:

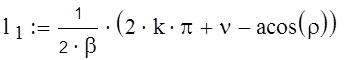                                                                                        (6.1)

                                                                                        (6.2)

               Длина отрезка линии                                l₁=0.05948 м  

               Длина короткозамкнутого шлейфа        l₂=0.06834 м

7. Определение значений параметров элементов согласующего устройства

по диаграмме полных сопротивлений.

 

Определяю нормированное значение сопротивления нагрузки

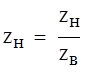
                                (7.1)

                                                                     

       Нахожу на диаграмме (см. Приложение 1) точку, соответствующую z_н  , по                    пересечению окружности   R=0.47  и  дуги   X=-0.87 .                 

       Провожу  радиус через точку z_н до пересечения со шкалой относительных                   расстояний, поворачиваю луч по часовой стрелке до окружности R=1 и

       делаю отсчет относительной длины отрезка линии:

                                                                              

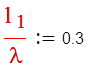
       На диаграмме  короткозамкнутому концу линии соответствует точка R=0                             (верхняя точка диаграммы). По шкале расстояний отсчитываю относитель-

        ное значение длины шлейфа:    

                                                                           

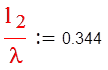
      Таким образом, получаю искомые длины отрезка линии и шлейфа: