Анализ гармонического процесса в отрезке радиотехнического кабеля генератора мощностью 55 Вт и внутренним сопротивлением 75 Ом

графика определен коэффициент затухания на данной частоте:

2. Моделирование генератора, нагрузки и отрезка радиочастотного кабеля

           Высокочастотный генератор гармонических колебаний мощностью   и внутренним сопротивлением   можно заменить эквивалентным сосредоточенным двухполюсником, состоящей из последовательно включённых источника гармонического напряжения  и резистора с сопротивлением  с комплексными характеристиками:

                                                                                              (2.1)

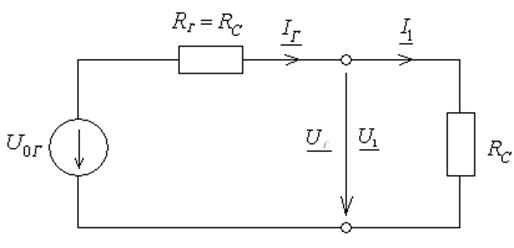
Рис. 2.1. Схема замещения генератора с согласованной нагрузкой

         Под значением мощности в более узком смысле понимают значение мощности генератора, отдаваемой им в согласованную нагрузку (рис. 2.1.). Если генератор моделируется активным двухполюсником с источником напряжения, то его мощность , очевидно, равна

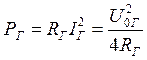                                                     (2.2)

   Отсюда напряжение холостого хода активного двухполюсника :

                            (2.3)

Сосредоточенная нагрузка отрезка кабеля в установившемся гармоническом процессе моделируется неавтономным сосредоточенным двухполюсником с комплексными характеристиками:

                                                                                                   (2.4)

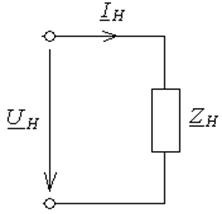
Рис. 2.2. Нагрузка кабеля

Отрезок радиочастотного кабеля моделируется отрезком однородной линии той же длины, определяемой двумя характеристическими параметрами: характеристическим сопротивлением   и постоянной (коэффициентом) распространения .

     Значение коэффициента найдено из графика частотных зависимостей выбранного кабеля (рис.1.2): .

     Коэффициент фазы (волновое число)обратно пропорционален длине электромагнитной волны в кабеле:

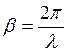,                                  (2.5)

которая  в (коэффициент укорочения длины волны) раз короче электромагнитной волны в вакууме , длина последней, как известно, определяется по формуле:

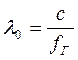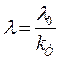                        ,                              (2.6)

где  - округленное значение скорости электромагнитной волны в вакууме.

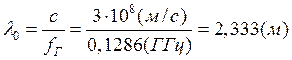
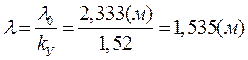
      Коэффициент фазы, таким образом, равен:

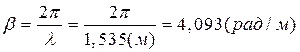
      Длину отрезка  найдем из заданного соотношения  :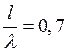

                                                               (2.7)

      Если в согласованном режиме значение мощности, потребляемой отрезком кабеля, пренебрежимо мало в сравнении со значением мощности генератора, то его можно удовлетворительно моделировать отрезком однородной линии без потерь той же длины. Применение такой довольно грубой модели оправдано, если затухание отрезка кабеля в согласованном режиме не превышает ; при этом с погрешностью не более 5%.

       В нашем случае:

    ;

 Т.е. отрезок кабеля можно удовлетворительно моделировать отрезком однородной линии без потерь той же длины.

3. Расчет распределения действующих значений (огибающих) напряжения и тока вдоль нагруженного отрезка линии без потерь

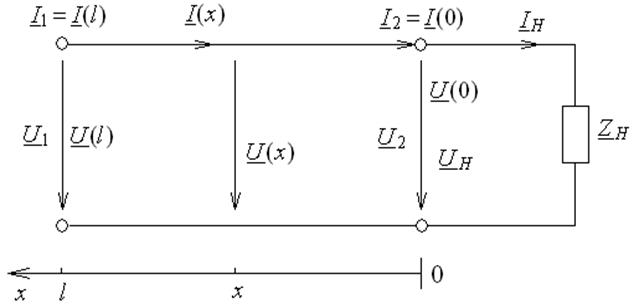
Рис. 3.1. Схема нагруженного отрезка линии

В качестве исходных возьмем выражения с экспоненциальными функциями мнимого аргумента, определяющие комплексы действующих значений напряжения  и тока  в произвольном сечении с координатой (0 ≤ x ≤ l), отсчитываемой от конца отрезка линии  без потерь (рис.3.1).

                                                               (3.1)

                                                                  (3.2)    

   где через  иобозначены комплексы действующих значений напряжения и тока соответствующих прямобегущих волн в том же сечении:

                       и                                 (3.3)

  причем

                                                                                 (3.4)

Вычисляя модули выражений и , после несложных преобразований получаем искомые функции распределений ,(огибающих волн напряжения