Расчет переходного тока при помощи одной из форм интеграла Дюамеля

Задание: На вход схемы подается импульсное напряжение , заданное графиком. Рассчитать при помощи одной из форм интеграла Дюамеля переходный ток, указанный на схеме стрелкой и построить график его изменения в функции времени.

Исходные данные:

Параметры элементов:

;

;

;

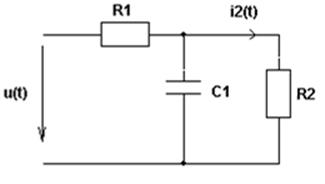
       Рис. 1. Заданная схема

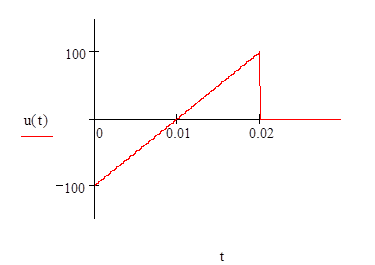
Рис. 2. График входного воздействия

Решение:

1)  Запишем аналитическое выражение входного воздействия.На промежутке функция может быть представлена выражением . Вне этого промежутка функция  равна нулю. Таким образом, входное воздействие можно представить  линейной комбинацией функций включения:

2)  Найдем значение входного воздействия в нуле:

3)  Найдем производную от входного воздействия на промежутке :

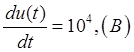 при

4)  Определим переходную проводимость :

1 способ. Метод, основанный на расчете переходного процесса.

Переходная проводимость какой-либо ветви схемы численно равна току в этой ветви при подключении цепи к источнику постоянного напряжения в 1 В.

Таким образом,

A)  Расчет принужденной составляющей (момент времени ):

                      

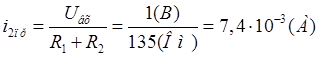
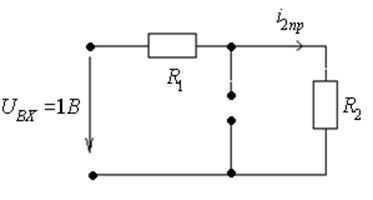
Рис. 3. Схема замещения при

B)  Определение:

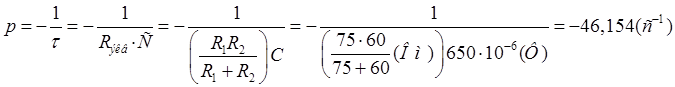
С) Независимые начальные условия (законы коммутации):

;

D) Зависимые начальные условия (момент времени ):

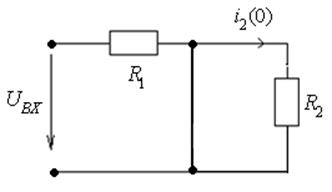Составим резистивную схему на момент коммутации. В резистивной схеме конденсатор заменяется источником напряжения, значение которого определяется из независимых начальных условий. Т. к. при расчете переходных характеристик начальные условия выбираются нулевыми, то ветвь с конденсатором будет просто закороткой.

 Рис. 4. Резистивная схема замещения при

Как видно из схемы (рис. 4) ветвь с резистором оказывается закороченной, поэтому ток .

E)  Любой ток в переходном процессе можно представить как сумму свободной и принужденной составляющих. В частности ток  равен:

При  получаем:

 

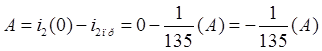
F) Таким образом переходная проводимость имеет вид:

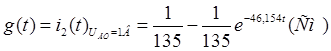
2 способ. Операторный метод.

Переходную проводимость какой-либо ветви схемы можно определить как оригинал от операторного выражения для тока в этой ветви, если на входе цепи действует единичный источник напряжения.

;

Составим операторную схему замещения для данной цепи. С учетом нулевых начальных условий конденсатор заменяется операторным сопротивлением  .

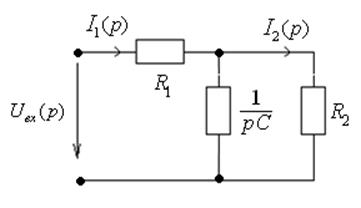
                                                     Рис. 5. Операторная схема замещения

Единичное входное воздействие имеет изображение:

;

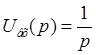Ток на входе цепи можно найти как:

 ,

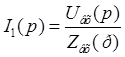где   - входное сопротивление цепи в операторной форме.

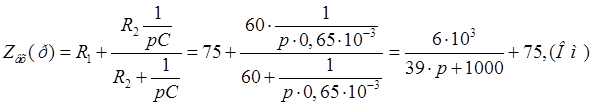
Тогда ток на входе цепи равен:

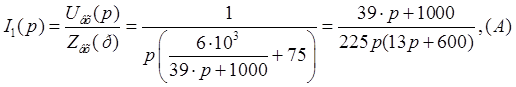
Ток в ветви с резистором  можно найти по методу делителя токов:

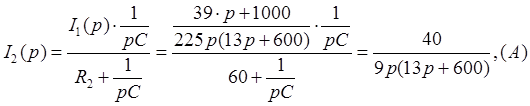
Переходя к оригиналу, получаем:

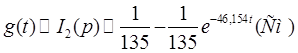
Таким образом, результаты обоих способов решения совпадают, что говорит о правильности выполненных расчетов.

 4)   Запись решения по интервалам.

На промежутке  ток  будет определяться следующим выражением :

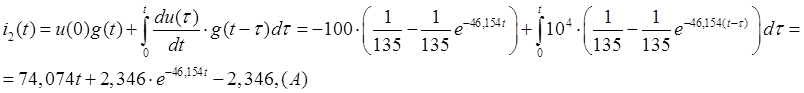 На промежутке   выражение для тока будет иметь следующий вид:

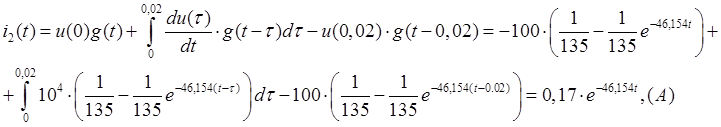
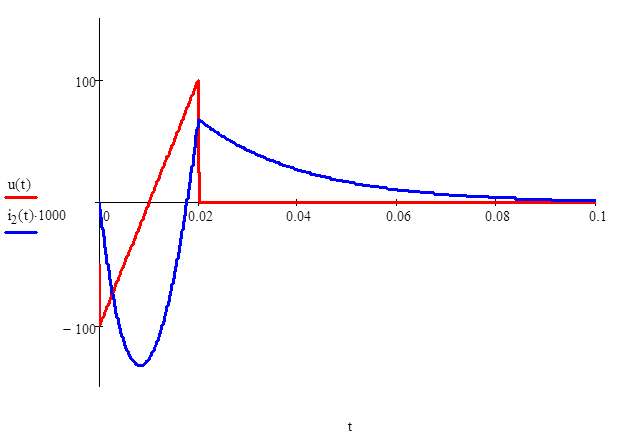
График тока  имеет вид:

                                                                            

                                                                            

                                                                            

                                                     Рис. 6. График изменения тока