Елементи теорії похибок геодезичних вимірів, страница 3

Вважаючи різниці випадковими похибками, можна сподіватися, що при достатньо великій кількості подвійних вимірювань сума їх буде близькою до нуля. Якщо ж це спостерігається, то можна допустити, що у вимірюваннях є систематичні похибки.

Відношення δ = [а]/п є виразом у середньому систематичної похибки у одній різниці вимірювань.

Виключивши величину систематичної похибки з різниць, одержимо нове значення: δ₁ = α₁ - δ; δ₂ = α₂-δ; δ₃=α₃-δ;....δ_n = α_n - δ.

У такому разі середню квадратичну похибку різниць вимірювань можливо визначити за формулою:

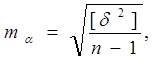а середню квадратичну похибкою одного вимірювання - за формулою:

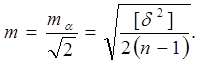Приклад визначення

                                                                            α=+4                 α²=2128

Середня квадратична похибка різниць вимірювань:

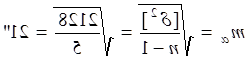Середня квадратична похибка однієї пари вимірювань:

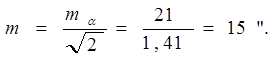Індивідуальні завдання для самостійних розрахунків.

№ вимірювань	Результати вимірювань довжини лінії, l	Δ=l-x	Δ2
1	195,02	+2	4
2	195,01	+1	1
3	194,99	-1	1
4	195,00	0	0
5	194,98	-2	4
6	195,01	+1	1
7	195,02	+2	4
8	194,97	-3	9
9	194,99	-1	1
10	195,01	+1	1
11	194,98	-2	4
12	195,02	+2	4
13	194,99	-1	1
14	195,01	+1	1
15	195,03	+3	9
16	194,98	-2	4
17	194,99	-1	1
18	194,98	-2	4
19	195,02	+2	4
20	195,01	+1	1
n=2	Дійсне значення х=195,00	Σ+випадків=10 Σ-випадків=9	Σ=59

Середня квадратична похибка вимірювань за формулою:

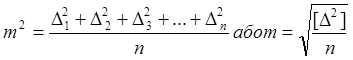де ,  Δ - похибка одного вимірювання;

      n - кількість вимірювань.

Отже                          

При виконанні геодезичних вимірювань з вимогою високої точності значення m приймають за граничну похибку. При менших вимогах точності вимірювань за граничну (допустиму) похибку приймають 2m, або навіть 3m. У нашому прикладі m=1,70 см; m=3,40 см; m=5,10 см.

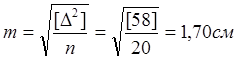Використовуючи формулу m_{граничне} =2m=3,40 см, перевіримо на даному ряді вимірювань властивості випадкових похибок. Найбільша похибка у наведеному прикладі 3,40 см. Цим підтверджується перша властивість випадкових похибок: випадкові похибки не можуть перевищувати за абсолютним значенням визначеної межі.

Позитивних похибок у даному ряді вимірювань 10, від'ємних  - 9, тобто кількість позитивних і від'ємних похибок приблизно порівно, а це підтверджує  другу властивість випадкових похибок: у масиві вимірювань позитивні і від'ємні похибки зустрічаються порівну.

У даному прикладі мали похибки, які не перевищують m, зустрічаються у 10 випадках, тобто у половині вимірювань, а похибки які перевищують 2m, тобто 3,40 см, взагалі відсутні і це підтверджує третю властивість випадкових похибок: малі за абсолютним значенням похибки зустрічаються значно частіше ніж великі.

Четверта властивість випадкових похибок та, що при необмежено великій кількості вимірювань середнє арифметичне з випадкових похибок прямує до нуля, тобто:

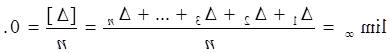Індивідуальні завдання для аудиторних занять.