Елементи теорії похибок геодезичних вимірів, страница 2

Рішення. Абсолютну похибку визначаємо як різницю двох вимірювань Δ = 124,62-124,56=0,06 м=6 см.

Знаходимо відносну похибку δ = Δ/l = 0.06/(124.56+124.62)/2=0.06/124.59=1/2076/

Висновок. Відносна похибка відповідає вимозі 1/2076<1/2000, а це означає, що вимірювання виконано з достатньою точністю для місцевості першої категорії, а тим більше для місцевості інших категорій.

Приклад.Дані дві лінії з дійсними значеннями Х₁=150,70м ,X₂=480,60м

Виміряли ці лінії і отримали їх значення l₁=150.84м. l₂=480,88м

Абсолютні похибки вимірювань дорівнюють: для першої лінії Δ=150,84-150,70=0,14, для другої лінії Δ=480,88-480,60-0,28м

Необхідно визначити відносні похибки і вказати яка з ліній виміряна точніше.

Рішення. δ₁=0,14/150,70=1/1076;      δ₂=0,28/480,60=1/1716.

Висновок. Друга лінія виміряна точніше тому що 1/1716<1/1076.

За точністю вимірювань перша лінія відноситься до місцевості третьої категорії (1/1076<1/1000), а друга до місцевості другої категорії (1/1716<1/1500).

2.  Середня квадратична похибка виміру. Гранична похибка

Дуже часто при виконанні геодезичних вимірювань дійсне значення величини, яку визначають, (Х) бува невідоме. У такому випадку за точне значення величини приймають її середнє арифметичне значення (L). (найвірогідніше значення). Різниця між окремими вимірюваннями і найвірогіднішим значенням називаються похибками v=l-L. Ці похибки характеризуються наступними властивостями:

1)  сума найвірогідніших похибок дорівнює нулю, тобто [v]=0;

2)  сума квадратів найвірогідніших похибок є мінімум [v²]=min.

Для прикладу вирішимо завдання, використовуючи ряд вимірювань величини, значення якої невідоме.

Необхідно визначити:

1.  Середнє арифметичне значення кута.

2.  Середню квадратичну похибку окремого вимірювання.

3.  Середню квадратичну похибку середнього арифметичного.

4.  Граничну похибку.

№ в-нь	Результати вимірювань	Відхилення від найвірогіднішого значення	Квадрати відхилень V2
1	222027'38"	-2	4
2	222027'56"	+16	256
3	222027'41"	+1	1
4	222027'33"	-7	49
5	222027'27"	-13	169
6	222027'39"	-1	1
7	222027'44"	+4	16
8	222027'34"	-6	36
9	222027'52"	+12	144
10	222027'36"	-4	16
N=10	L=222027'40"	[v]=0	[v2]=692

1.  Середнє арифметичне значення кута L=222⁰27'40".

2. 

Середнє квадратична похибка окркмого вимірювання визначаються за формулою

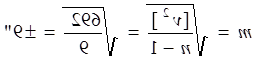3.  Середня квадратична похибка середнього арифметичного визначаються за формулою:

4. 
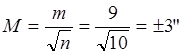
Гранична (максимальна допустима) похибка дорівнює при:

m=±9"; 2m=±18"; 3m=±27".

При вимірюванні або розмітці на місцевості горизонтального кута, яке найчастіше виконується за допомогою теодоліта, вимірювання виконується обов'язково парну кількість разів (2,4,6 і така далі) і обов'язково при двох положеннях вертикального кругу приладу: круг вправо (КП) і круг вліво (КЛ). Ця вимога диктується тим, ця вимога диктується тим, що прилади можуть мати нерівномірну розмітку (градуювання) лімбу горизонтального круту і саме цим заходом (двома положеннями вертикального кругу) ця нерівномірність, а отже і похибка вимірювання, самознищується.

Якщо кожна величина виміряна двічі і вимірювання рівноточні, то середню квадратичну похибку одного вимірювання можливо визначити з різниць, одержаних для кожної рари вимірювань.

Середню квадратичну похибку однієї різниці визначають за формулою:

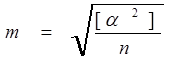α   різниця подвійних вимірювань;

n - кількість пар вимірювань.

У зв'язку з тим,. що вимірювання рівноточні. середня квадратична похибка кожного вимірювання повинна бути у (2)^1/2 разів меншою, тобто

m_α = m(2)^1/2, де m - середня квадратична похибка одного вимірювання.

()тже, т = т_α:/ 2 = [α² ]/2n.