Поиск условного минимума нелинейной функции многих переменных при линейных ограничениях

Пусть для хранения единицы і -го товара требуется V м³ складской емкости и при этом общая емкость складских помещений равна М. Тогда ограничение по складской емкости для хранения средних запасов можно записать в виде неравенства:

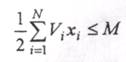 (4.31)

Запишем теперь функцию суммарных издержек:

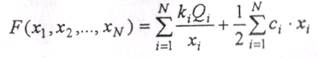 (4.32)

Таким образом, имеем постановку задачи поиска условного минимума нелинейной функции многих переменных (4.32) при линейных ограничениях (4.31). Для решения этого класса задач используемся метод неопределенных множителей Лагранжа, который заключается в следующем.

Составим функцию Лагранжа:

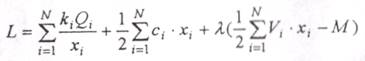 (4.33)

Неопределенный    множитель    X,    входящий    в    эту    функцию,    обладает следующими свойствами:

Х=0 при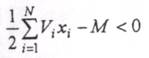 (4.34) для случая, когда объем средних запасов

превышает складскую емкость;

X X) при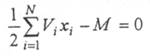 (4.35) для случая, когда объем средних запасов

равен складской емкости.

Таким образом, в указанных случаях (4.34) и (4.35) обеспечивается равенство исходной функции (4.32) и функции Лагранжа (4.33), т.е. равенство Y-L. Но безусловный минимум функции достигается только при условии (4.35) - равенстве необходимой и имеющейся складской емкости.

Найдем этот минимум, определив для каждой переменной функции Лагранжа частные производные и приравняв их нулю, получим следующую систему уравнений:

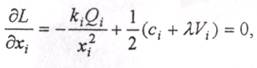
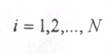    (4.36)

Решая ее, определяем оптимальные объемы поставок:

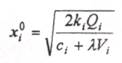 (4.37)

Подставим выражение (4.37) в уравнение ограничений по складской емкости (4.35). В результате получаем:

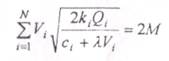 (4.38)

В равенсткс (•) W) пес неличины, кроме неопределенного множителя X, известны. КореиІ. лого уравнения Х=Хо X) можсі быть найден нулем решения этого уравнения методом приближенных вычислений. Найденное таким образом решение определяет объем оптимальных запасов в условиях принятого выше ограничения по складской емкости:

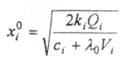 (4.39)

Анализ формулы (4.39) показывает, что при xq =0 (для случая, когда складских емкостей достаточно для размещения запасов) оптимальный объем поставки и соответственно минимум функции суммарных издержек совпадают с обычными оптимальными неличинами, рассчитанными без ограничения на складскую емкость. 11ри ао > 0 (для случая, когда складских емкостей недостаточно для размещения запасов) оптимальный объем поставки (запасов) будет меньше, чем рассчитанный без ограничений на складскую емкость.

Соответственно,  увеличатся суммарные издержки  по сравнению с  их безусловным   минимумом.   Их   приращение   по   сравнению   с   оптимальным