Исследование и синтез корректирующего устройства системы автоматического управления

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА АППМ

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА

ПО ТЕОРИИ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

на тему: «Анализ и синтез линейной непрерывной системы автоматического управления»

Вариант 2-5

Выполнил: Минулин Артем Раильевич

Факультет: МТ

Группа: ТМ-601

Проверил: Нос О. В.

НОВОСИБИРСК

2009

1. ИСХОДНЫЕ ДАННЫЕ

1.1. Структура и параметры исходной нескорректированной САУ

Табл. 1.1

Алгебраические уравнения исходной САУ

Табл. 1.2

Параметры динамических звеньев исходной САУ

v - задающее воздействие,

f – возмущающее воздействие,

x_i – входная переменная i-го звена,

y_i – выходная переменная i-го звена,

y– выходная (управляемая) переменная САУ.

1.2. Система обыкновенных дифференциальных уравнений, описывающих динамику звеньев исходной САУ

,(1.1)

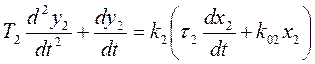,(1.2)

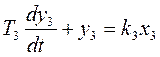,(1.3)

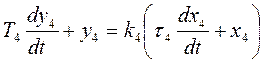.(1.4)

1.3. Желаемые показатели качества переходных процессов и статическая точность регулирования

- допустимая статическая ошибка ;

- максимально допустимое время регулирования ;

- максимально допустимое перерегулирование ;

2. АНАЛИЗ НЕПРЕРЫВНОЙ ЛИНЕЙНОЙ САУ

2.1. В соответствии с табл. 1.1 составить структурную схему линейной нескорректированной САУ

Рис. 2.1  Схема нескорректированной CАУ

2.2. На основании уравнений (1.1)-(1.4) записать уравнения в операторной форме записи в общем виде и с учетом численных значений.

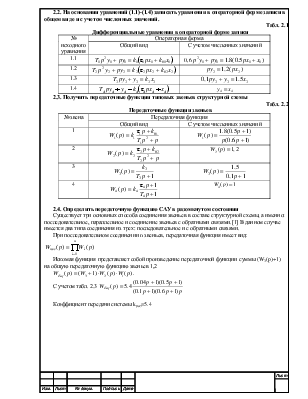
Табл. 2.1

Дифференциальные уравнения в операторной форме записи

2.3. Получить передаточные функции типовых звеньев структурной схемы

Табл. 2.2

Передаточные функции звеньев

2.4. Определить передаточную функцию САУ в разомкнутом состоянии

Существует три основных способа соединения звеньев в составе структурной схемы, а именно: последовательное, параллельное и соединение звеньев с обратными связями.[1] В данном случае имеется два типа соединения из трех: последовательное и с обратными связями.

При последовательном соединении n звеньев, передаточная функция имеет вид: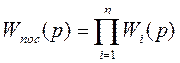

Искомая функция представляет собой произведение передаточной функции суммы (W₃(p)+1)  на общую передаточную функцию звеньев 1,2

.

С учетом табл. 2.3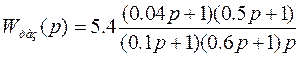

Коэффициент передачи системы k_раз=5.4

2.5. Записать передаточные функции замкнутой САУ по задающему (v) и возмущающему (f) воздействиям

Замкнутая передаточная функция по задающему воздействию имеет вид: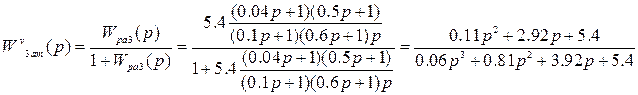

Замкнутая передаточная функция по возмущающему воздействию по (2.2), с учетом числовых значений, имеет вид: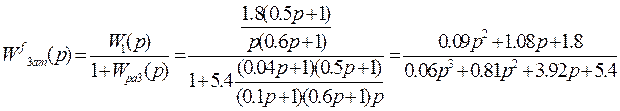

2.6. При помощи алгебраического критерия устойчивости Гурвица проверить условие устойчивости нескорректированной САУ.

Критерий Гурвица гласит:

Для того чтобы линейная система была устойчива, необходимо и достаточно, чтобы главный определитель матрицы Гурвица и все его диагональные миноры были положительными.[1]

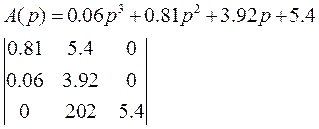
Для данной САУ.    

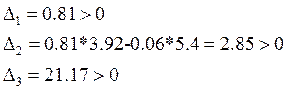
Следовательно, система является устойчивой.

3. СИНТЕЗ ПОСЛЕДОВАТЕЛЬНОГО КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА НА ОСНОВАНИИ МЕТОДА ЖЕЛАЕМОЙ ЛАЧХ

3.1. Изобразить ЛАЧХ нескорректированной системы L_нс(ω).

ЛАЧХ строится по следующему алгоритму [2]:

- На оси абсцисс отмечаются точки lg(T₁^-1)=0,22дек, lg(T₃^-1)=0.3дек, lg(T₂^-1)=1дек,lg(T₄^-1)=1.4дек

- До частоты, соответствующей абсциссе 0,22 строится прямая с наклоном -20 дБ/дек. Пересекающая ось ординат в точке 20lg(k_pa3)=20lg(5.4)=14.65дБ  

- Далее, строится прямая под углом -40дБ/дек. до частоты, соответствующей абсциссе 0,3.

- Затем строится прямая под углом -20 дБ/дек. до частоты, соответствующей абсциссе 1.

- Из точки с абсциссой 1 проводится прямая под углом -40 дБ/дек, до частоты, соответствующей абсциссе 1.4

-Далее строится прямая под углом -20дБ/дек

3.2. Построить желаемую ЛАЧХ скорректированной системы L_жел(ω) и ЛАЧХ корректирующего устройства L_ку(ω).

Построение начинается из области средних частот. По номограммам[3] определяется соотношение ω_ср и  по заданному значению , где  =20% и Pmax=1,07. 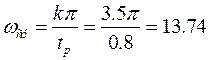с^-1. Запас устойчивости по модулю ΔL(ω)=+25 дБ. Через точку lg(ω_ср)=1.138дек проводится прямая с наклоном -20 дБ/дек.

Далее определяется коэффициент передачи скорректированной системы 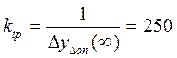. Через точку (0, 20lg()=48дб) проводится из области низких частот прямая под углом -20 дБ/дек, до пересечения с нею строится прямая с наклоном -40дб/дек из точки принадлежащей границе НЧ и СЧ желаемой ЛАЧХ. Прямая, лежащая в области высоких частот, проводится параллельно соответствующей прямой исходной ЛАЧХ.[4]

ЛАЧХ корректирующего устройства определяется по формуле [4]

3.3 Определение передаточной функции корректирующего звена

Порядок определения функции  обратен порядку построения ЛАЧХ нескорректированной системы.[2] Коэффициенты T_i передаточной функции корректирующего звена определяются по формуле .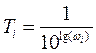

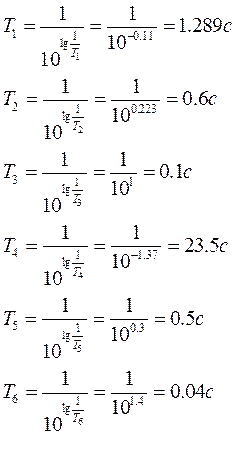
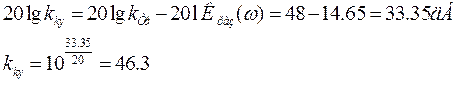
В результате имеем:

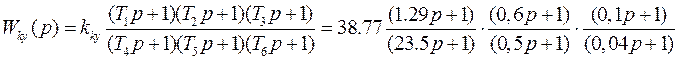
Проверка K_Tp:

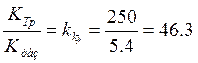
3.4 Составление схемы САУ с учетом корректирующего устройства

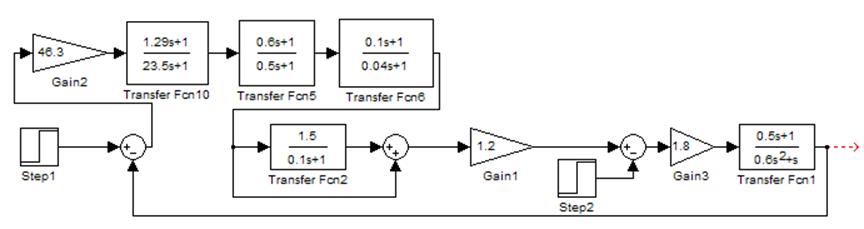
Рис. 3.1 Схема скорректированной САУ

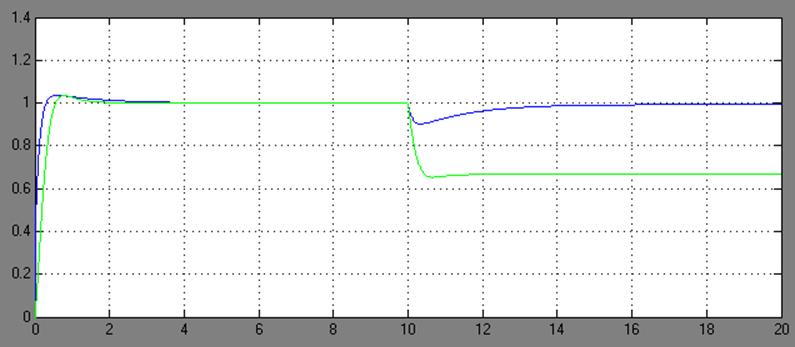
Рис. 3.1.1 Скорректированная и нескорректированная САУ

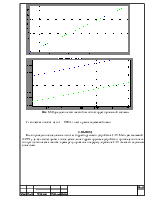
3.5 Моделирование управляющего воздействия

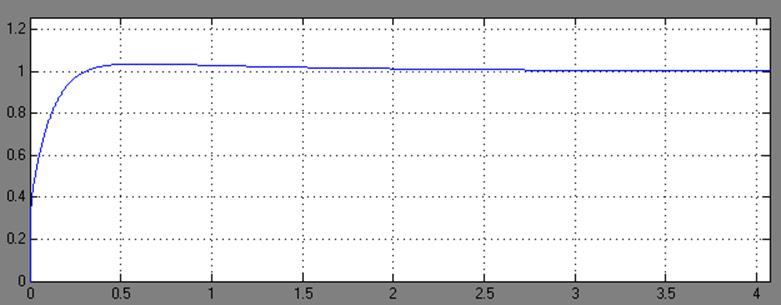
Рис. 3.2 Прямые показатели качества переходной скорректированной системы

Время регулирования ;   0,18с<0,8с

Перерегулирование . 4,3%<20%

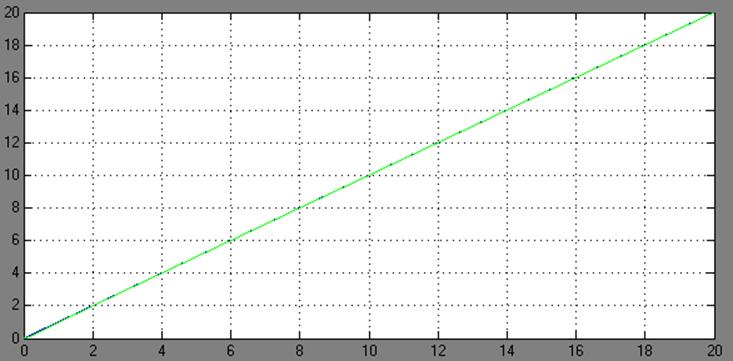
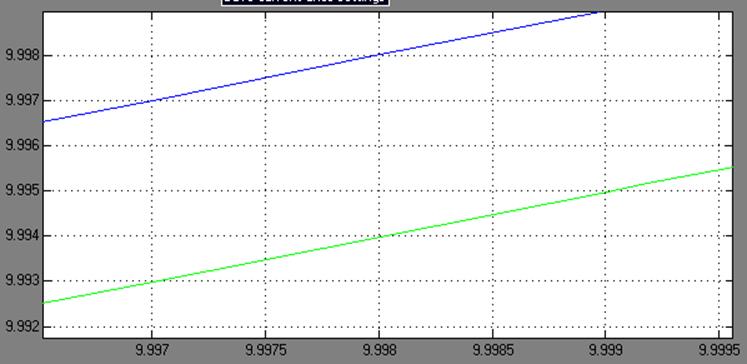
Рис. 3.3 Определение статической ошибки скорректированной системы