








Министерство образования и науки Российской Федерации
НГТУ
Кафедра ТМ
Расчетно-графическое задание по дисциплине
Теория автоматизированного управления
Факультет: МТ
Группа: ТМ-12
Студент: Павленко М.Н.
Преподаватель: Каплин В.И.
Новосибирск, 2004
Задание на расчетно-графическую работу.
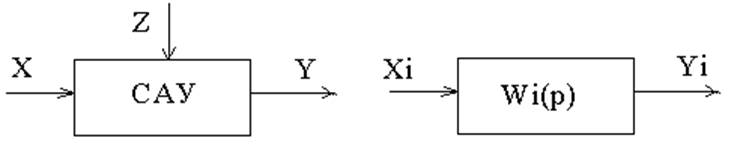
рис.1. рис.2.
Задана система автоматического управления (рис.1), состоящая из четырех элементов (рис.2, I=1,2,3,4), где приняты следующие обозначения:
Х – задающее воздействие;
У – выходное воздействие;
Z – возмущающее воздействие;
Xi – выходное воздействие i-го элемента;
Yi – выходная величина i-го элемента.
Элемент i=1 является объектом управления, остальные элементы относятся к управляющей (усилительно-преобразующей) части САУ.
Динамические свойства элементов в общем случае описывается дифференциальными уравнениями:
T1 d2y1+ dy1 = K1(t1dx1 + k01x1);
dt2 dt dt
T2 d2y2+ dy2 = K2(t2dx2 + k02x2);
dt2 dt dt
T3 dy3+ y3 = K3 x3;
dt
T4 dy4+ y4 = K4(t4dx4 + x4);
dt dt
где Ki,Ti,t1- параметры элементов.
Из таблицы 1 берем 0-ой вариант уравнений связей, где для каждого элемента определены входные воздействия в виде комбинаций выходных величин других элементов.
х3=(х-у)-y4, х4=х2=у3, х1=у2-z, у1=y.
Из таблицы 2 берем значения коэффициентов и постоянных времени соответствующих 1-му варианту:
К1=1 t1=1 T1=0.8 k01=0
К2=0.5 t2=1 T2=0.2 k02=0
К3=0.5 T3=0
К4=0.5 t4=0.4 T4=0.3
Часть 1. Анализ исходной системы.
1.1.
 |
1.2. Конкретизируем выражения, подставив в них значения коэффициентов и постоянных времени равных нулю и единице.
T1 d2y1+ dy1 = dx1 ;
dt2 dt dt
T2 d2y2+ dy2 = K2dx2 ;
dt2 dt dt
y3 = K3 x3;
T4 dy4+ y4 = K4(t4dx4 + x4);
dt dt
1.3. Полученные дифференциальные уравнения запишем в операторном виде:
T1 P2y1 + Py1 = Px1 ;
T2 P2y2 + Py2 = K2Px2 ;
y3 = K3 x3;
T4 Py4 + y4 = K4(t4Px4 + x4);
1.4. По полученным дифференциальным уравнениям запишем выражения передаточных функций:
W1 = y1= 1 ;
x1 T1 P+ 1
W2 = y2= K2 ;
x2 T2 P+ 1
W3 = y3= K3 ;
x3
W4 = y4= K4 (t4P+1) ;
x4 T4 P+ 1
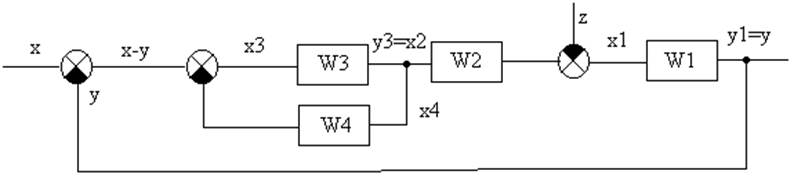
1.5. Преобразуем полученную структурную схему так, чтобы у нас схема была одноконтурной:
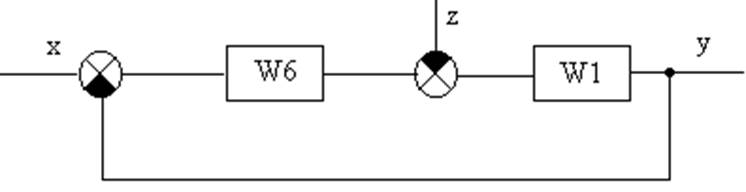 |
1.6.
 |
1.7. Определим передаточную функцию разомкнутой системы Краз.
Wраз = K6 (t6P+1) ;
(T6 P+ 1)(T5 P+ 1)(T1 P+ 1)
Краз= K6 = 0.2.
1.8. Определяем передаточные функции замкнутой системы по задающему и возмущающему воздействиям:
WXY = Wраз = Kраз (t6P+1) =
1+ Wраз (T6 P+ 1)(T5 P+ 1)(T1 P+ 1) + Kраз (t6P+1)
= Kраз (t6P+1) ;
T6 T5 T1P3+(T1(T5 +T6 )+ T6 T5)P2+(T1+T5+T6)P+1+ Kраз (t6P+1)
1 1 .
WZY = (-1) T1P+1 = (-1) T1P+1 =
1+ Wраз (T6 P+ 1)(T5 P+ 1)(T1 P+ 1) + Kраз (t6P+1)
= (-1)(T6 P+ 1)(T5 P+ 1) ;
T6 T5 T1P3+(T1(T5 +T6 )+ T6 T5)P2+(T1+T5+T6)P+1+ Kраз (t6P+1)
1.9. Запишем уравнение замкнутой системы в операторной и дифференциальной форме:
[T6 T5 T1P3+(T1(T5 +T6 )+ T6 T5)P2+(T1+T5+T6)P+1+ Kраз (t6P+1)]Y = = [Kраз (t6P+1)]X + [(T6 P+ 1)(T5 P+ 1)] Z ;
d3y d2y dy dy =
T6 T5 T1 dt3+(T1(T5 +T6 )+ T6 T5) dt2+(T1+T5+T6) dt+y+ Kраз(t6dt+1)
= dx + d2z + dz + ;
Kраз (t6dt+1) T6 T5 dt2 (T5 +T6) dt
1.10. Проверим устойчивость по критерию Гурвица-Рауса, для этого запишем операторный полином при выходной координате Y в виде:
anpn + an-1pn-1 +…+ a1p + a0 ;
T6 T5 T1P3+(T1(T5 +T6 )+ T6 T5)P2+(T1+T5+T6)P+1+ Kраз (t6P+1);
Для устойчивости линейной системы необходимо и достаточно, чтобы все коэффициенты операторного полинома при Y были положительными:
a3= T6 T5 T1=0.0512>0
a2= T1(T5 +T6 )+ T6 T5 =0.48>0
a1= T1+T5+T6 + Kраз t6=1.38>0
a0= Kраз =0.2>0
Условие устойчивости выполняется.
1.11. Определим предельное значение коэффициента усиления разомкнутой системы из условия устойчивости системы:
T6 T5 T1 Kраз = (T1(T5 +T6 )+ T6 T5 ) (T1+T5+T6 + Kраз t6);
0.0512 Kраз =1.38(1.32+ Kраз 0.3);
Kраз = -5.021.
1.12. Вычислим установившиеся (статические) ошибки по задающему и возмущающему воздействиями, приняв для задающего ступенчатую и линейную функции, а для возмущающего – только ступенчатую функцию. Статические ошибки определяем в процентном отношении к модулю ступенчатого воздействия и скорости изменения линейного воздействия.
WXE(P)= 1 = T6 T5 T1P3+(T1(T5 +T6 )+ T6 T5)P2+(T1+T5+T6)P+1=
1+ Wраз (T6 P+ 1)(T5 P+ 1)(T1 P+ 1) + Kраз (t6P+1)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.