Другие предметы \ Теория автоматического управления

Анализ системы автоматического управления с управляющей (усилительно-преобразующей) частью, страница 2

=           T6 T5 T1P3+(T1(T5 +T6 )+ T6 T5)P2+(T1+T5+T6)P+1                  ;   

    T6 T5 T1P3+(T1(T5 +T6 )+ T6 T5)P2+(T1+T5+T6)P+1+ Kраз (t6P+1)

                        1          .                                   

WZE(P)= (-1) T1P+1(-1) =            T6 T5 P2+ (T5+T6)P+1                       =

             1+ Wраз             (T6 P+ 1)(T5 P+ 1)(T1 P+ 1) + Kраз (t6P+1)

=                                  T6 T5 P2+ (T5+T6)P+1                                         ;

   T6 T5 T1P3+(T1(T5 +T6 )+ T6 T5)P2+(T1+T5+T6)P+1+ Kраз (t6P+1)

eсmx= lim WXE(P) X =0.83;

eсmz= lim WZE(P) Z =0.83;

eлинx= lim WXE(P)  1 =       ;

                               P

1.13.  Определяем показатели качества переходных процессов, выполнив моделирование на ЭВМ по программе COMPAS. Для моделирования используется структурная схема, в которой все элементы представлены в виде типовых звеньев, содержащихся в программе COMPAS.

Переходные процессы получаем как реакцию системы на единичные ступенчатые задающие и возмущающие воздействия.


На рис.3 представлен график переходного процесса при подаче постоянного сигнала по уравнению и возмущению, а на рис.4 представлен график переходного процесса при подаче сигнала постоянной скорости.

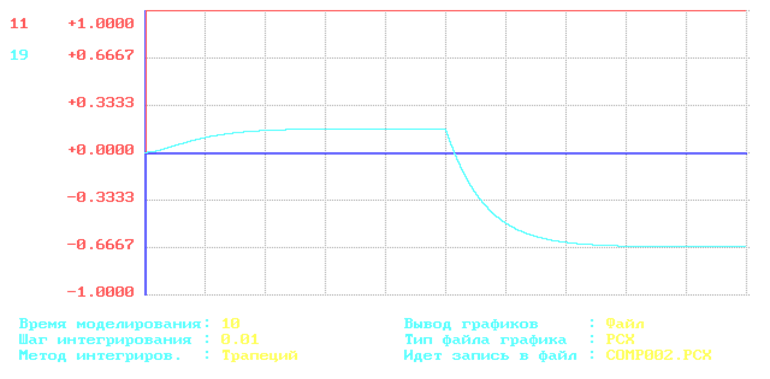
рис.3 График переходного процесса исходной системы при единичном ступенчатом воздействии (задающем и возмущающем)


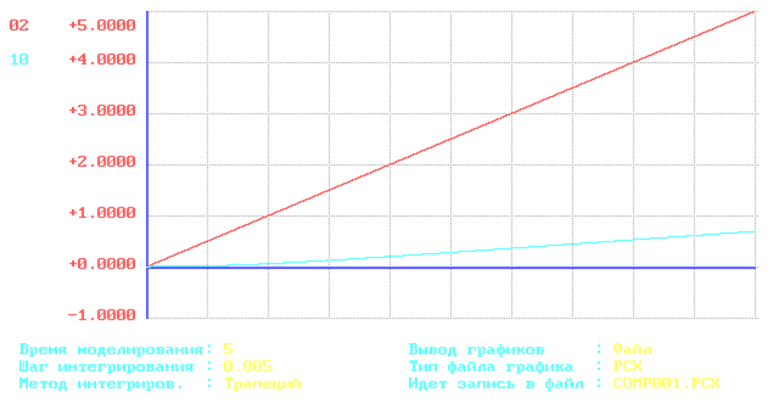рис.4 График переходного процесса исходной системы при подаче сигнала постоянной скорости.

1.14. Анализируя исходную систему, заключаем, что:

        1) время переходного процесса tпп= 2,3с.

        2) пере регулирование отсутствует.

        Статическая ошибка при подаче единичного ступенчатого сигнала по задающему воздействию равна- 0.83, что соответствует результатам вычисления. Статическая ошибка при подаче сигнала постоянной скорости по задающему воздействию-    , что также численно совпадает с ошибкой, полученной аналитическим путем.

Часть 2. Синтез корректирующего звена.

2.1. Строим ЛАХ исходной системы.

W0 (P) =                K0 (t6P+1)               =          K0    (0.3P+1)               ;

               (T6 P+ 1)(T5 P+ 1)(T1 P+ 1)    (0.32P+1)(0.2P+1)(0.8P+1)

K0= 0.2;

        При построении ЛАХ системы, состоящей из последователь- ных типовых звеньев учитывается, что логарифм произведения есть сумма логарифмов, поэтому для каждого звена можно построить ЛАХ, а затем просуммировать и получить ЛАХ всей системы. Для этого найдем частоты каждого из звеньев.

20lgK0= -13.98;

w1=   1  = 3;    w2=   1   =3;  w3=   1  = 5; w4=  1  = 1.25;

       0.3                   0.32                0.2               0.8

        На оси ординат обозначим точку 20lgk0, а на оси абсцисс значения частот сопряжения.

        Из точки 20lgk0 на оси ординат проводим прямую под углом 0[дБ/дек] (так как система не содержит в себе интегрирующее звено).

        Далее проводим прямую под углом -20[дБ/дек] из точки lgw1 до сопряжения lgw4, а потом проводим излом асимптоты равным     -40[дБ/дек].

2.2.  Построение желаемой ЛАХ.

Желаемую ЛАХ строят по рекомендации. Так при построении

ЛАХ исходной системы у нас график  пересек ось абсцисс. Так как  длительность переходного процесса в скорректированной системе должна быть на порядок меньше, чем в исходной, то принимаем

wср =2p/tпп=13.65.   

2.3.  ЛАХ корректирующего звена.

ЛАХ корректирующего определяем как разность между

желаемой и исходной системы.

        Получив ЛАХ корректирующего элемента, определяем по ней выражение передаточной функции и значение ее параметров:

WК =     100 (0.8P+1) (0.2P+1)   ;

               (0.3 P+ 1)(0.01 P+ 1)

2.4.  Построим структурную схему скорректированной системы,


включив корректирующий элемент в структурную схему исходной системы.

2.5.  Определим показатели качества переходных процессов скорректированной системы при единичном ступенчатом сигнале (рис.5) и при подаче сигнала постоянной скорости (рис.6).


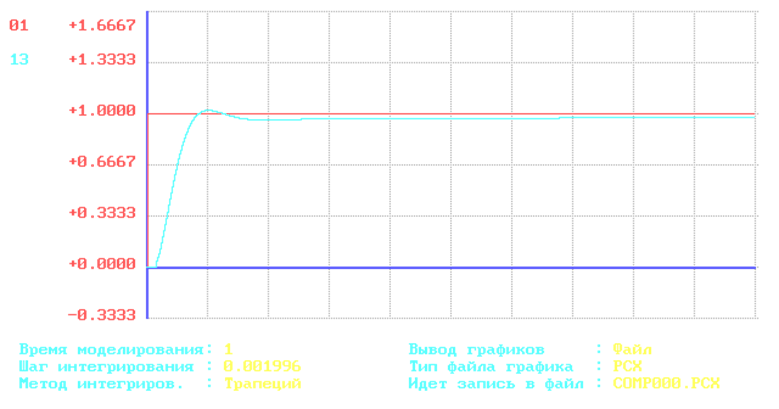Рис.5. График переходного процесса скорректированной системы при ступенчатом единичном задающем воздействии.


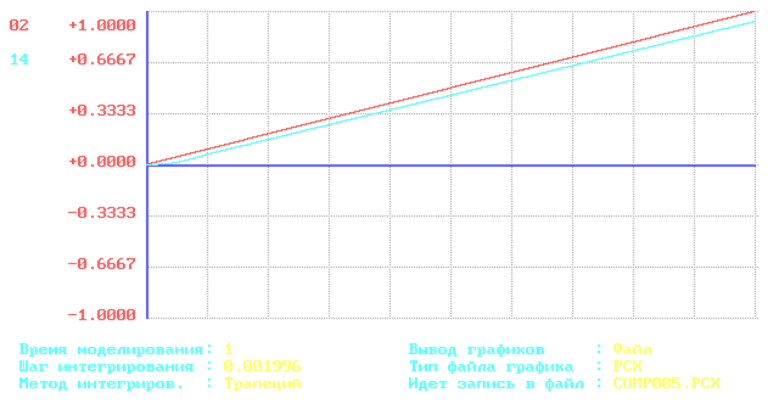Рис.6. График переходного процесса скорректированной системы при подаче сигнала постоянной скорости.

2.6.  Вычислим установившиеся (статические) ошибки по задающему и возмущающему воздействиям, приняв для задающего ступенчатую функцию и линейную функции, а для возмущающего – только ступенчатую функцию. Статические ошибки определяем в процентном отношении к модулю ступенчатого воздействия и скорости изменения линейного воздействия.

Передаточная функция скорректированной системы:

Wраз  =                51                    ;

    (0.01P+1)(0.32P+1)

WXE(P)=     1      =    (0.01P+1) (0.32P+1)    ;

             1+ Wраз       (0.01P+1)(0.32P+1)+51

                        1          .                                   

WZE(P)= (-1) T1P+1(-1) =              (0.01P+1)(0.32P+1)               ;

             1+ Wраз                 ((0.8P+1)(0.32P+1)+52)(0.01P+1)

eсmx= lim WXE(P) X =0.02;

eсmz= lim WZE(P) Z =0.02;

eлинx= lim WXE(P)  1 =       ;

                               P

Сравниваем показатели качества переходных процессов и

статические ошибки скорректированной системы в соответствии с заданными требованиями.

        В процессе моделирования мы получили системы, удовлетворяющую следующим требованиям к качеству:

1.     статическая ошибка при отработке единичного ступенчатого воздействия (задающего и возмущающего) не должна превышать 5% от заданного значения управляемой величины.

2.     длительность переходного процесса обеспечена на порядок меньше, чем у исходной системы.

3.     статическая ошибка при подаче сигнала постоянной скорости равна 4%.

Показатели качества и статические ошибки скорректированной системы удовлетворяют изложенным выше требованиям.

Скачать файл