Анализ механизма поперечно-строгального станка

Записываем уравнение замкнутости  второго контура в векторной форме:

L₇+L₆-L_3с = 0

Проецируем эти векторы на оси координат и получаем систему уравнений

-L_3Сcos(j₃) + L₆cos(j₆) + L₇cos(j₇) =0

-L_3Сsin(j₃) + L₆sin(j₆) + L₇sin(j₇) =0                                                                              (2.2)

Находим неизвестные L₇ и j₇:

j₇ = arctg [(L₃sin(j₃) - L₆sin(j₆))/ (L₃cos(j₃) - L₆cos(j₆))]

L₇ = (L₃cos(j₃) - L₆cos(j₆))/cos(j₇)

j₇ =180 + arctg [(0,68×sin(115,62) – 0,65×sin(90))/ (0,68×cos(115,62) –0,65×cos(90))] = 164,.96^о,

L₇ = (0,68×cos(115,62) - ,65×cos(90))/cos(164,96) = 0,0927м

Рассмотрим третий контур Е-В-С-Е (рис. 2.4).

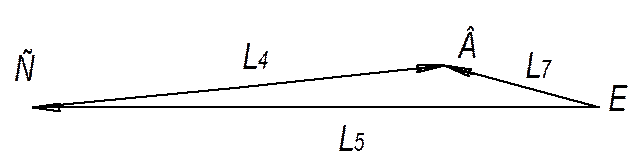
Рис. 2.4. Контур Е-В-С-Е

 Записываем уравнение замкнутости третьего контура в векторной форме:

L₄+L₅-L₇ = 0

Проецируем эти векторы на оси координат и получаем систему уравнений

-L₇cos(j₇) + L₄cos(j₄) + L₅cos(j₅) =0

-L₇sin(j₇) + L₄sin(j₄) + L₅sin(j₅) =0                                                                               (2.3)

Находим неизвестные L₅ и j₄:

j₄ = arcsin [(L₇sin(j₇) – L₅sin(j₅))/L₄]

L₅ = (L₇cos(j₇) – L₅cos(j₅))/cos(j₄)

j₄ = 5.75^о,

L₅ = 0.3284м

Для определения координат центров масс звена 4 запишем замкнутый контур:

 О₂-О₁-S₃-О₂:

L_O2S3+L_O1S3-L₀=0

Проецируем эти векторы на оси координат и получаем систему уравнений:

L_O2S3sin(j₃)+L_O1S3sin(O₁S₃E)-L₀sin(j₀)=0

L_O2S3cos(j₃)+L_O1S3cos(O₁S₃E)-L₀cos(j₀)=0

Координаты центра масс звена 3:

S_3X= L₀cos(j₀)- L_O2S3cos(j₃)

S_3Y= L₀sin(j₀)- L_O2S3sin(j₃)                                                                                    (2.4)

S_3Y= 0.0329, S_3X=0.0448

Для определения координат центров масс звена 4 запишем замкнутый контур:

C-D-S4-C

L_S4D+L₅-L_CS4=0

Проецируем эти векторы на оси координат и получаем систему уравнений:

L_S4Dsin(S₄DF)+L₅sin(j₅)-L_CS4sin(j₄)=0

L_S4Dcos(S₄DF)+L₅cos(j₅)-L_CS4cos(j₄)=0

Координаты центра масс звена 4:

S_4X= L_CS4cos(j₄)- L₅cos(j₅)

S_4Y= L_CS4sin(j₄)- L₅sin(j₅)                                                                                      (2.5)

S_4Y= 0.012, S_4X=0.2091

2.3.5. Находим скорости звеньев.

Для нахождения скоростей звеньев надо взять производную от системы

уравнений 2.1 и в результате получим:

-j’₁L₁sin(j₁)+L’₃cos(j₃)-L₃sin(j₃)j’₃ –L₀sin(j₀)j’₀=0

j’₁L₁cos(j₁)+L’₃sin(j₃)-L₃cos(j₃)j’₃ +L₀cos(j₀)j’₀=0

cos(j₀)=0, j’₁= -1, т.к. угловая скорость звена направлена по ходу часовой стрелки.

Вычтем, из каждого угла j₃ и получим:

-L₁sin(j₁-j₃)+L’₃₁=0            

L₁cos(j₁-j₃)-L₃₁ j’₃=0

Из этой системы уравнений находим скорость камня вдоль кулисы L’₃₁ , и

угловую скорость кулисы т.к. считаем, что угловая скорость первого звена

равна  1.

 L’₃₁=L₁sin(j₁-j₃)

j’₃=L₁cos(j₁-j₃)/L₃₁

Находим скорости звеньев второго контура. Для нахождения скоростей звеньев

второго контура надо взять производную от системы уравнений 2.2 и в

результате получим:

-L₄sin(j₄)* j’₄-L₃ sin(j₃)* j’₃-b’=0                                                 2.5

L₄cos(j₄)* j’₄+L₃cos(j₃)* j’₃=0

Если мы из каждого угла вычтем угол j_4, то получим:

-L₃ sin(j₃-j₄)* j’₃-b’=0

L₄j’₄+L₃cos(j₃-j₄)* j’₃=0

Из этой системы уравнений находим скорость ползуна b’ и угловую скорость

шатуна j’₄.

 b’=-L₃ sin(j₃-j₄)* j’₃

 j’₄= (L₃cos(j₃-j₄)* j’₃)/ L₄

Скорости центров масс, так же находим дифференцированием соответствующих

систем .

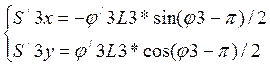
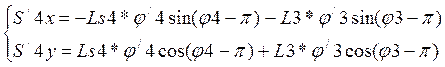
Скорость S5x совпадает со скоростью т. b.

Находим ускорения звеньев первого контура.

Для нахождения ускорения звеньев первого контура надо взять производную

от системы уравнений 2.4 и в результате получим:

-L₁cos(j₁)+L’’₃₁cos(j₃)-L’₃₁sin(j₃)* j’₃- L’₃₁sin(j₃)* j’₃- L₃₁cos(j₃)* (j’₃)²-

-L₃₁sin(j₃)* j’’₃=0   2.4

-L₁sin(j₁)+L’’₃₁sin(j₃)+L’₃₁cos(j₃)* j’₃+ L’₃₁cos(j₃)* j’₃- L₃₁sin(j₃)*(j’₃)²+

+L₃₁cos(j₃)* j’’₃=0

 Если мы из каждого угла вычтем угол j_{3 ,}то получим:

-L₁cos(j₁-j₃)+L’’₃₁cos(j₃-j₃)-L’₃₁sin(j₃-j₃)* j’₃- L’₃₁sin(j₃-j₃)* j’₃-

-L₃₁cos(j₃-j₃)* (j’₃)²-L₃₁sin(j₃-j₃)* j’’₃=0                                                              

-L₁sin(j₁-j₃)+L’’₃₁sin(j₃-j₃)+L’₃₁cos(j₃-j₃)* j’₃+ L’₃₁cos(j₃-j₃)* j’₃-

-L₃₁sin(j₃-j₃)*(j’₃)²+L₃₁cos(j₃-j₃)* j’’₃=0

-L₁cos(j₁-j₃)+L’’₃₁-L₃₁* (j’₃)²=0                                                              

-L₁sin(j₁-j₃)+L’₃₁ j’₃+ L’₃₁ j’₃-L₃₁ j’’₃=0

Из этой системы уравнений находим ускорение камня вдоль кулисы L’’₃₁ и

угловое ускорение кулисы j’’₃ т.к. считаем ,что первое звено движется

равномерно с постоянным по модулю угловым ускорением.

L’’₃₁=L₁cos(j₁-j₃)+ L₃₁* (j’₃)^2­

j’’₃=(L₁sin(j₁-j₃)-2L’₃₁ j’₃)/L₃₁

 

Находим ускорения звеньев второго контура.

Для нахождения ускорения звеньев второго контура надо взять производную

от системы уравнений 2.5 и в результате получим:

-L₄cos(j₄)* (j’₄)²-L₄ sin(j₄)* j’’₄- L₃cos(j₃)* (j’₃)²- L₃ sin(j₃)* j’’₃-b’’=0    2.5

-L₄sin(j₄)* (j’₄)²+L₄cos(j₄)* j’’_4­- L₃sin(j₃)* (j’₃)²+ L₃ cos(j₃)* j’’₃=0

Если мы из каждого угла вычтем угол j_{4 ,} то получим:

-L₄cos(j₄-j₄)* (j’₄)²-L₄ sin(j₄-j₄)* j’’₄- L₃cos(j₃-j₄)* (j’₃)²- L₃ sin(j₃-j₄)* j’’₃-b’’=0   

-L₄sin(j₄-j₄)* (j’₄)²+L₄cos(j₄-j₄)* j’’_4­- L₃sin(j₃-j₄)* (j’₃)²+ L₃ cos(j₃-j₄)* j’’₃=0

и она принимает вид:

-L₄ (j’₄)²- L₃cos(j₃-j₄)* (j’₃)²- L₃ sin(j₃-j₄)* j’’₃-b’’=0   

L₄ j’’_4­- L₃sin(j₃-j₄)* (j’₃)²+ L₃ cos(j₃-j₄)* j’’₃=0

Из этой системы уравнений находим ускорение ползуна b’’ и угловое ускорение

 шатуна j’’₄.

b’’=-L₄ (j’₄)²- L₃cos(j₃-j₄)* (j’₃)²- L₃ sin(j₃-j₄)* j’’₃   

j’’₄­= (L₃sin(j₃-j₄)* (j’₃)²- L₃ cos(j₃-j₄)* j’’₃)/ L₄=0

Подробные расчёты приведены в приложении.

Находим ускорения центра масс звеньев механизма.

Для нахождения ускорения центра масс звеньев надо взять  производную от

систем уравнений, скоростей центра масс звеньев и в результате получим:

Ускорение центра масс звена 3:

 S’’_3x= -j’’₃L₃sin(j₃-p)/2 – (j’3)²L3 cos(j₃-p)/2

 S’’_3y= j’’₃L₃ cos(j₃-p)/2-+ (j’3)²L3sin(j₃-p)/2

S’’_4x=[ Ls4(-j’’₄sin(j₄-p) – (j’4)² cos(j₄-p)) – L3(j’’₃sin(j₃-p) + (j’3)² cos(j₃-p ))]

S’_4y=[ Ls4(-j’’₄cos(j₄-p) – (j’4)² sin(j₄-p)) – L3(j’’₃cos(j₃-p) + (j’3)² sin(j₃-p))]

2.4 Графическое определение положений, скоростей,

ускорений звеньев механизма.

2.4.1 Алгоритм графического построения планов положений.

Построение планов положениё производим следующим образом.

1.  Выбираем масштабный коэффициент длин m= 0.001 м/мм и рассчитываем

чертёжные размеры звеньев табл.2.1

Таблица 2.1  

2.  Отмечаем на чертеже неподвижные точки О₁, О₂ , рисуем в них вращательные

кинематические пары;

3.  На расстоянии У от точки О₁ проводим траекторию движения ползуна 5;

4.  Проводи окружность О₁А, которая является траекторией движения точки А;

5.  На траектории движения точки А отмечаем крайние положения кулисы 3 и

откладываем длину О₂В;

6.  На траектории движения точки С отмечаем крайние положения ползуна 5 и

соединив крайние точки С с точками В крайних положений кулисы получим

крайние положения шатуна 4;

7.   Зная полную длину хода Н ползуна 5 находим начало и конец рабочего хода, от

 крайних положений точки С откладываем внутрь отрезка Н длину Н/10;

8.  Методом засечек строим положения шатуна 4, кулисы 3 и кривошипа 1;

9.  Делим траекторию звена 1 на 12 частей начиная от левого крайнего