механизма, соответственно второе крайнее положение примем равным 270°
 2.2 Построение планов положений исследуемого механизма.
2.2 Построение планов положений исследуемого механизма.
1) Выбираем масштабный коэффициент длин mi= 0,0026 м/мм и рассчитываем чертежные размеры звеньев (табл.№1)
Таблица№1
|
ОА |
АВ |
ОС |
CD |
AS2 |
CS4 |
|
|
L,м |
0.13 |
0.52 |
0.13 |
0.52 |
0.26 |
0.26 |
|
L*m mm |
50 |
200 |
50 |
200 |
100 |
100 |
Планы положений строим следующим образом :
- Проведем окружности с центром в точке О радиусом ОА– траекторию движения по которой движется точка А и разделим эту окружность начиная от точки А0 (начало рабочего хода ) на12 частей. Точки деления обозначим А0…А11 в направлении движения кривошипа. Для каждого положения кривошипа строим план механизма методом засечек.
- С учетом координирующих размеров (X,Y) отмечаем на чертеже неподвижную точку О, проводим линию движения точки В радиусом АВ из каждой точки А находим соответствующее положение точки В аналогично и для точки Д радиусом СД из соответствующих точек С.
-
2.3 КИНЕМАТИЧЕСКОЕ ИССЛЕДОВАНИЕ МЕХАНИЗМА АНЛИТИЧЕСКИМ МЕТОДОМ
Сущность всех аналитических методов заключается в том, что линейные и угловые координаты, скорости и ускорения точек звеньев механизма определяются в виде аналитических выражений. Исходными данными для вывода выражений является: структурная схема механизма, изображающая механизм в любом (расчетном) положении, исключая крайние; размеры звеньев; заданные положения обобщенных координат механизма; законы движения обобщенных координат механизма во времени. Если последнее не задано, то уравнения записываются в функции обобщенных координат, т.е. определяют не сами искомые функции, а их аналоги.
В данном курсовом проекте применим метод замкнутых векторных контуров для исследуемого механизма.
В соответствие с предложенным методом поступаем следующим образом.
Схема механизма расположена в прямоугольной системе координат, начало которой для первого контура поместим в точку О, а во втором контуре в точку О и так как эти контуры совпадают и различаются лишь положением во времени то расчет ведем по одному контуру, а второй берем из первого с учетом знака. Со звеньями механизма связываем векторы так, чтобы их последовательность образовала два замкнутых контура: ОАВО и ОСDО.
Углы определяющие положение векторов, будем отсчитывать от направления оси X, в направлении хода часовой стрелки.
Отметим что контур ОСDO идентичен контуру ОАВО, далее мы будем проводить расчеты для контура ОАВО, а величины для контура ОСDO будем подбирать из соотношений:
1: A0-C6;A1-C7;A2-C8;A3-C9;A4-C10;A5-C11;A6-C0;A7-C1;A8-C2;A9-C3;A10-C4;A11-C5.
2: B0-D6;B1-D7;B2-D8;B3-D9;B4-D10;B5-D11;B6-D0;B7-D1;B8-D2;B9-D3;B10-D4;B11-D5. ![]()
3: S20-S46;S21-S47;S22-S48;S23-S49;S24-S410;S25-S411;S26-S40;S27-S41;S28-S42;S29-S43;
S210-S44;S211-S45.
 Для контура ОАВО:
Для контура ОАВО:
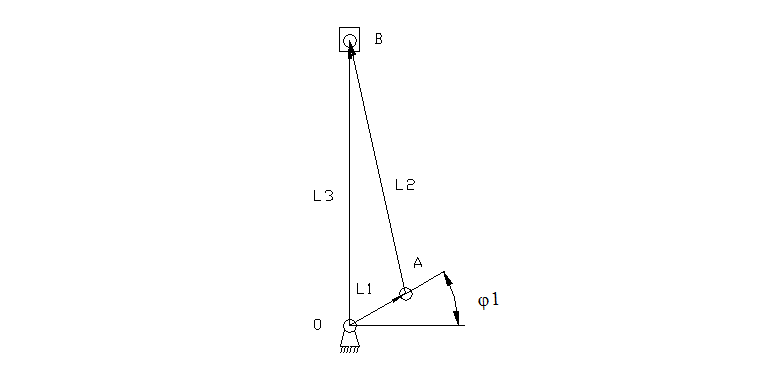
![]() Этому уравнению
соответствуют два уравнения проекций на оси координат:
Этому уравнению
соответствуют два уравнения проекций на оси координат:
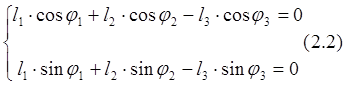
![]()
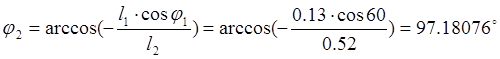
Для контура OCDO:
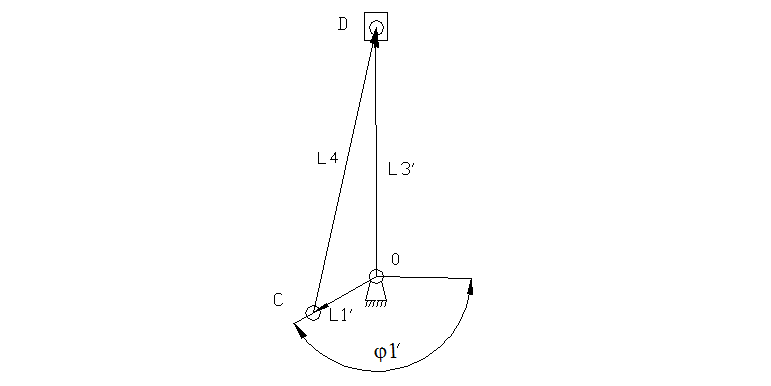
![]() Этому уравнению
соответствуют два уравнения проекций на оси координат:
Этому уравнению
соответствуют два уравнения проекций на оси координат:
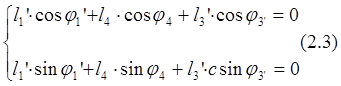
![]()
![]()
2. Расчет центров масс.

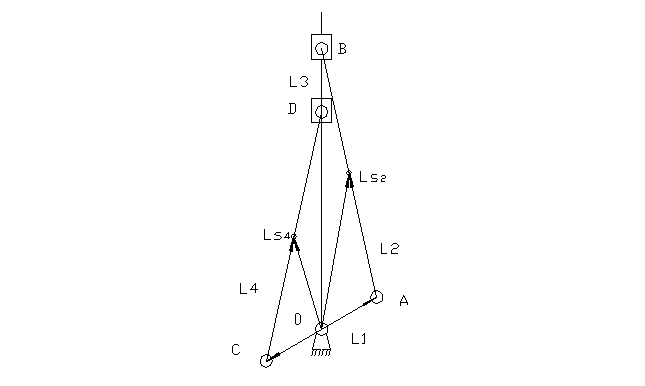
В проекциях на оси получим:
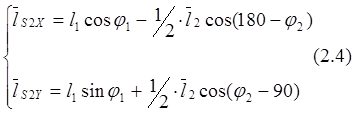
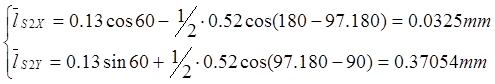
Положение точек и центров масс контура OCBO определяются подстановкой
в соотношения (2,1).
 Рассчитанные
величины сведем в таблицу №2
Рассчитанные
величины сведем в таблицу №2
Таблица №2
|
L1 |
L2 |
L3 |
j1 |
j2 |
j3 |
j1' |
j4 |
L3' |
|||
|
0,13 |
0,52 |
0,65 |
90 |
90 |
90 |
90 |
90 |
0,39 |
|||
|
0,13 |
0,52 |
0,628505 |
60 |
97,18076 |
90 |
120 |
82,81924422 |
0,4033382 |
|||
|
0,13 |
0,52 |
0,572666 |
30 |
102,5039 |
90 |
150 |
77,49608338 |
0,44266623 |
|||
|
0,13 |
0,52 |
0,503488 |
0 |
104,4775 |
90 |
180 |
75,52248781 |
0,50348784 |
|||
|
0,13 |
0,52 |
0,442666 |
-30 |
102,5039 |
90 |
210 |
77,49608338 |
0,57266623 |
|||
|
0,13 |
0,52 |
0,403338 |
-60 |
97,18076 |
90 |
240 |
82,81924422 |
0,62850481 |
|||
|
0,13 |
0,52 |
0,39 |
-90 |
90 |
90 |
270 |
90 |
0,65 |
|||
|
0,13 |
0,52 |
0,403338 |
-120 |
82,81924 |
90 |
300 |
97,18075578 |
0,62850481 |
|||
|
0,13 |
0,52 |
0,442666 |
-150 |
77,49608 |
90 |
330 |
102,5039166 |
0,57266623 |
|||
|
0,13 |
0,52 |
0,503488 |
-180 |
75,52249 |
90 |
360 |
104,4775122 |
0,50348784 |
|||
|
0,13 |
0,52 |
0,572666 |
-210 |
77,49608 |
90 |
390 |
102,5039166 |
0,44266623 |
|||
|
0,13 |
0,52 |
0,628505 |
-240 |
82,81924 |
90 |
420 |
97,18075578 |
0,4033382 |
|||
|
S2X |
S2Y |
S4x |
S4Y |
||||||||
|
0 |
0,39 |
0 |
0,13 |
||||||||
|
0,0325 |
0,370544 |
-0,0325 |
0,145377 |
||||||||
|
0,056291651 |
0,318833 |
-0,05629 |
0,188833 |
||||||||
|
0,065 |
0,251744 |
-0,065 |
0,251744 |
||||||||
|
0,056291651 |
0,188833 |
-0,05629 |
0,318833 |
||||||||
|
0,0325 |
0,145377 |
-0,0325 |
0,370544 |
||||||||
|
0 |
0,13 |
0 |
0,39 |
||||||||
|
-0,0325 |
0,145377 |
0,0325 |
0,370544 |
||||||||
|
-0,056291651 |
0,188833 |
0,056292 |
0,318833 |
||||||||
|
-0,065 |
0,251744 |
0,065 |
0,251744 |
||||||||
|
-0,056291651 |
0,318833 |
0,056292 |
0,188833 |
||||||||
|
-0,0325 |
0,370544 |
0,0325 |
0,145377 |
||||||||
И так для положения A1 разница значений графического и аналитического методов составит:
|
j1 |
j2 |
j1 ‘ |
j4 |
L3 |
L3’ |
S2X |
S2Y |
S4X |
S4Y |
|
|
Графически |
60 |
97 |
120 |
83 |
0.62849 |
0.4033 |
0.0325 |
0.372 |
-0.0325 |
0.14536 |
|
Аналитически |
60 |
97.1807 |
120 |
82.819244 |
0.628505 |
0.403382 |
0,0325 |
0,37054 |
-0,0325 |
0,14537 |
|
D,% |
0 |
0.0018 |
0 |
0 |
0 |
0 |
0 |
0.0039 |
0 |
0 |
 2.3.1 Определение
аналогов скоростей аналитическим методом.
2.3.1 Определение
аналогов скоростей аналитическим методом.
Аналитический метод основан на дифференцировании по общей координате уравнений (2.2) и (2.4) получим:
![]()
(2.5)
![]()
где![]() =1 аналог угловой
скорости звена 1.
=1 аналог угловой
скорости звена 1.
Из (2.5) вычисляем функции углов:
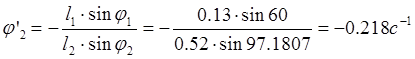
![]()
Аналоги скоростей центров масс звена 2 получим в проекциях
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.