Анализ и синтез линейной системы автоматического управления, состоящей из четырех элементов

Министерство образования и науки Российской Федерации

Федеральное агентство образования

Государственное учреждение высшего профессионального образования

«НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Кафедра АППМ

Курсовая работа

По дисциплине:

«Теория автоматического управления»

На тему:

«Анализ и синтез линейной системы автоматического управления»

Факультет:           МТ

Специальность:   2102

Группа:                 КП-32

Студент:               Калмыков И.И.

Преподаватель:    Нос О.В.

Работа защищена:_____________

НОВОСИБИРСК

2006г.

ИСХОДНЫЕ ДАННЫЕ

– номер варианта структурной схемы: 3

– номер варианта параметров объекта управления: 5

– допустимая статическая (скоростная) ошибка регулирования:

– допустимое время регулирования: T_{РЕГ.ДОП}= 1.2c

– допустимое максимальное перерегулирование: 25%.

Структурная схема САУ

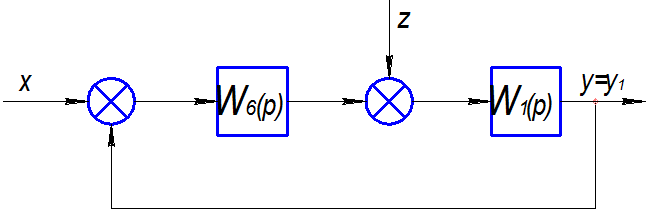
Дана система автоматического управления (рис.1), состоящая из четырех элементов (рис.2, i=1,2,3,4)

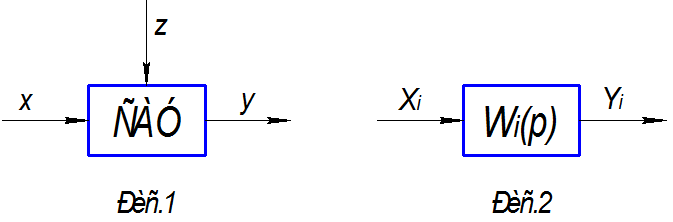
где  x – задающее воздействие,

y – управляемая величина,

z – возмущающее воздействие,

Xi – входное воздействие i-го элемента

Yi – выходная величина i-го элемента

Элемент i=1 является объектом управления. Остальные элементы относятся к управляющей части САУ.

Динамические свойства элементов в общем случае описываются дифференциальными уравнениями:

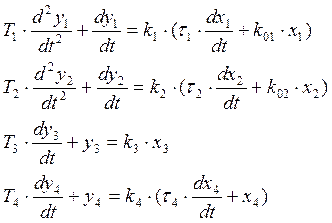
где ki, Ti, ti – параметры элементов.

Численные значения параметров:

                     

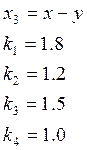
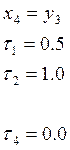
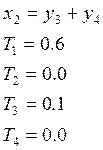
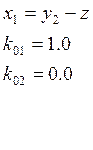
1.  АНАЛИЗ ИСХОДНОЙ СИСТЕМЫ.

1.1  По уравнениям связи строим структурную схему исходной нескорректированной САУ.

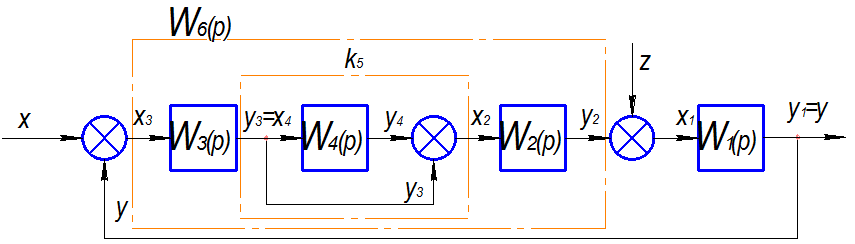
1.2  Уравнения в операторной форме в общем виде.

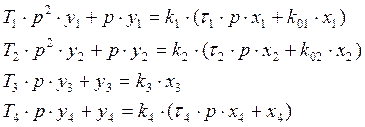
Уравнения в операторной форме с учетом численных значений.

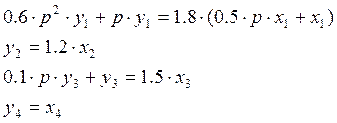
1.3  Передаточные функции элементов

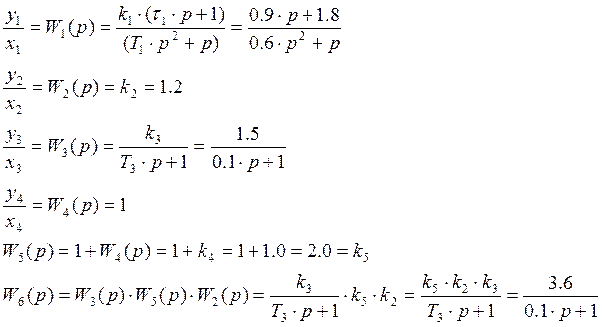
Полученную структурную схему преобразуем к виду:

1.4  Передаточная функция разомкнутой системы по задающему и возмущающему воздействиям.

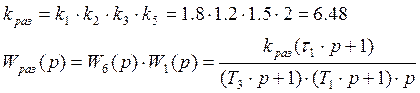
1.5  Передаточные функции замкнутой системы по задающему и возмущающему воздействиям.

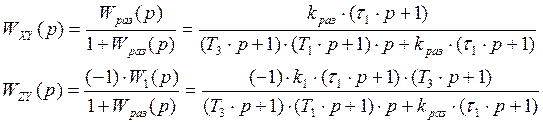
Определение ошибки регулирования по управляющему и возмущающему воздействиям при нулевых начальных условиях в случае приложения единичного ступенчатого воздействия.

Найдем передаточные функции относительно ошибок по управляющему и возмущающему воздействиях соответственно:

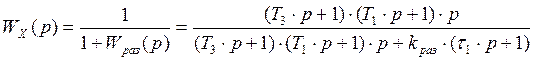
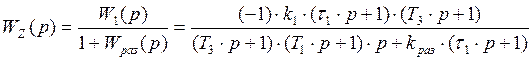
Статические ошибки (p=0) регулирования по управляющему и возмущающему воздействиях:

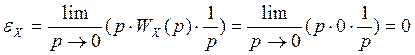
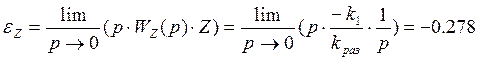
1.6 Проверка устойчивости системы по критерию Гурвица.

Так как в исследуемой САУ нет звена чистого запаздывания, то ее устойчивость можно установить по критерию Гурвица.

Формулировка критерия:

Для того, чтобы линейная САУ была устойчива, необходимо и достаточно, чтобы главный определитель матрицы Гурвица и все его n-1 диагональные миноры были положительными.

Матрица Гурвица составляется из коэффициентов характеристического уравнения заданной системы по определенным правилам.

Характеристическое уравнение заданной системы.

В критерии Гурвица характеристическое уравнение задается в виде операторного полинома при выходной координате Y:

Чтобы получить характеристическое уравнение заданной системы, приравняем нулю знаменатель заданной САУ и раскроем скобки:

,

Обозначим коэффициенты и найдем их значения:

,

,

,

.

Все коэффициенты характеристического уравнения положительны – необходимое условие устойчивости выполняется.

Составление матрицы Гурвица и определение устойчивости САУ.

Составляем матрицу Гурвица:

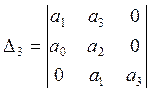
Условия устойчивости:

1) ,

2) .

По условию Гурвица, система является устойчивой.

1.7 Показатели качества переходных процессов при моделировании на ЭВМ. Для моделирования используется структурная схема, в которой все элементы представлены в виде типовых линейных звеньев.

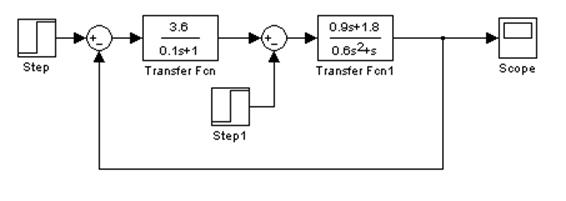
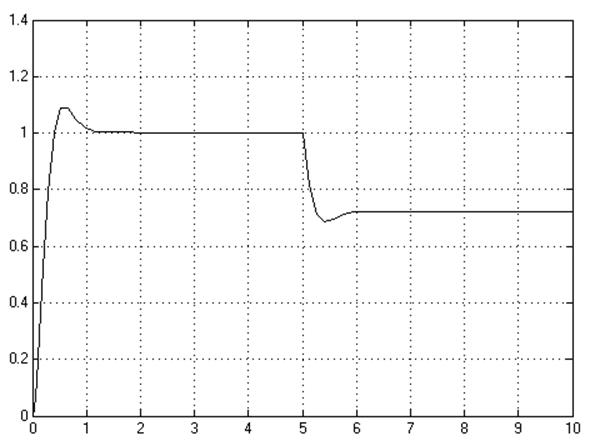
Переходная характеристика при задающем и возмущающем воздействиях    этой системы имеет следующий вид:

Переходная характеристика при возмущающем воздействии этой системы имеет следующий вид:

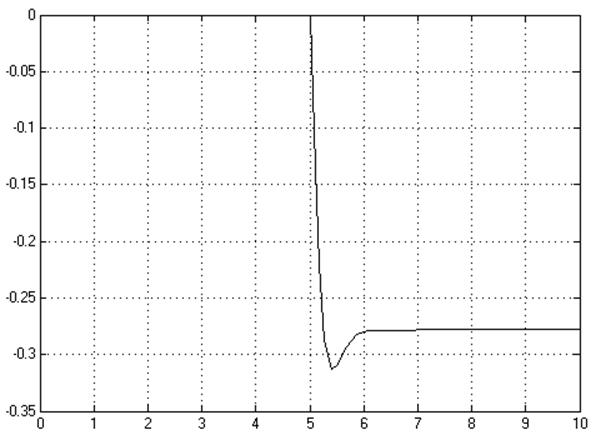
Вывод: 1) статическая ошибка при подаче единичного ступенчатого сигнала по задающему воздействию равна 0, что соответствует результатам вычисления.

2) статическая ошибка при подаче единичного ступенчатого сигнала по возмущающему воздействию равна -0.278, что также соответствует результатам вычисления.

3)

4) перерегулирование

2.  СИНТЕЗ ПОСЛЕДОВАТЕЛЬНОГО КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА ДЛЯ САУ.

2.1 Построение асимптотической ЛАЧХ нескорректированной системы –  в разомкнутом состоянии.

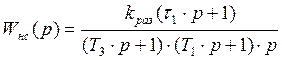
При построении ЛАЧХ системы, состоящей из последовательных типовых звеньев учитывается, что логарифм произведения есть сумма логарифмов, поэтому для каждого звена можно построить ЛАЧХ, а затем просуммировать и получить ЛАЧХ всей системы.

Для построения  рассчитываем необходимые параметры:

1) дБ

2) частоты сопряжения системы:

рад/с,

рад/с,

рад/с.

По оси абсцисс возьмем равномерный логарифмический масштаб . Поэтому частоты сопряжения пересчитываем в десятичные логарифмы частоты:

дек,

дек,

дек.

В координатной плоскости [L(w), lgw] при частоте w=1(lg1 = 0 дек) отложим ординату 20lgk и логарифмы частот сопряжения (рис. 2.1.).