Построение
ведем слева направо. В низкочастотной области (до минимальной частоты
сопряжения) асимптотическая LHC(w) – прямая
линия, проходящая под наклоном -20 дБ/дек, т.к. звено интегрирующее - ![]() , через точку с координатами (20lgk, 0). При
частотах сопряжения апериодических звеньев наклон LHC(w) изменяется на -20 дБ/дек, форсирующих - +20 дБ/дек. Таким образом,
асимптотическая LHC(w) представляет собой ломаную с наклонами -20, -40, -20
и -40 дБ/дек.
, через точку с координатами (20lgk, 0). При
частотах сопряжения апериодических звеньев наклон LHC(w) изменяется на -20 дБ/дек, форсирующих - +20 дБ/дек. Таким образом,
асимптотическая LHC(w) представляет собой ломаную с наклонами -20, -40, -20
и -40 дБ/дек.
2.2. Построение асимптотической желаемой ЛАЧХ - LЖ.
2.2.1. Построение низкочастотной зоны ![]() начинаем с определения требуемого
коэффициента передачи
начинаем с определения требуемого
коэффициента передачи ![]() .
.
![]() ;
; ![]()
Через точку (![]() , 0)
проводим прямую линию под наклоном -20 дБ/дек. Эта линия будет
соответствовать низкочастотной зоне желаемой ЛАЧХ.
, 0)
проводим прямую линию под наклоном -20 дБ/дек. Эта линия будет
соответствовать низкочастотной зоне желаемой ЛАЧХ.
2.2.2. Для построения СЧЗ необходимо определить частоту среза wС желаемой ЛАЧХ и ординаты начала и конца зоны.
При
заданном ![]() % по номограмме [1, рис. 5.26] определяем
% по номограмме [1, рис. 5.26] определяем ![]() , и по
, и по ![]() и
графику
и
графику ![]() находим соотношение между временем регулирования
и желаемой ЛАЧХ. То есть при
находим соотношение между временем регулирования
и желаемой ЛАЧХ. То есть при ![]() = 25%,
= 25%, ![]() = 1.18, а время регулирования:
= 1.18, а время регулирования:
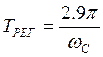 .
.
При заданном допустимом времени регулирования (TРЕГ.ДОП = 1.2) частоту среза найдем по формуле:
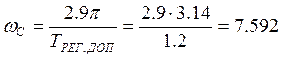 рад/с,
рад/с,
![]() .
.
Определим ординаты начала и конца среднечастотной зоны.
Ординаты начала и конца СЧЗ ориентировочно берутся
равными требуемому запасу устойчивости по модулю ![]() с
разными знаками. Требуемые запасы устойчивости по модулю и по фазе можно найти
по номограмме [1, рис. 5.27].
с
разными знаками. Требуемые запасы устойчивости по модулю и по фазе можно найти
по номограмме [1, рис. 5.27].
При ![]() требуемый запас
устойчивости по модулю
требуемый запас
устойчивости по модулю ![]() дБ, по фазе
дБ, по фазе ![]() град.
град.
Среднечастотная асимптота ![]() проводится
под наклоним -20 дБ/дек через точку на оси абсцисс, имеющую частоту в
логарифмическом масштабе
проводится
под наклоним -20 дБ/дек через точку на оси абсцисс, имеющую частоту в
логарифмическом масштабе ![]() . Начальную и конечную
ординаты принимаем равными ±16.5 дБ.
. Начальную и конечную
ординаты принимаем равными ±16.5 дБ.
2.2.4. Высокочастотная зона ![]() в
целях простоты реализации корректирующего устройства(регулятора) строится параллельно
ЛАЧХ исходной САУ, причем её наклон в целях фильтрации высокочастотных помех
должен составлять -20 дБ/дек или -40дБ/дек. Высокочастотную зону
проводим под наклоном -40 дБ/дек.
в
целях простоты реализации корректирующего устройства(регулятора) строится параллельно
ЛАЧХ исходной САУ, причем её наклон в целях фильтрации высокочастотных помех
должен составлять -20 дБ/дек или -40дБ/дек. Высокочастотную зону
проводим под наклоном -40 дБ/дек.
2.2.3. Среднечастотную и низкочастотную зону ![]() сопрягаем линией под наклоном -40 дБ/дек.
Этой графической операцией завершается построение асимптотической желаемой
ЛАЧХ.
сопрягаем линией под наклоном -40 дБ/дек.
Этой графической операцией завершается построение асимптотической желаемой
ЛАЧХ.
Передаточная функция “желаемого устройства” по виду ![]() :
:
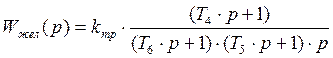
2.2.4.
Определим ЛАЧХ ![]() последовательного
корректирующего устройства графическим вычитанием ординат Lнс(w) из ординат
последовательного
корректирующего устройства графическим вычитанием ординат Lнс(w) из ординат
![]() .
.
2.3. Определение передаточной функции и соотношения параметров корректирующего устройства.
Передаточная
функция корректирующего устройства по виду ![]() :
:
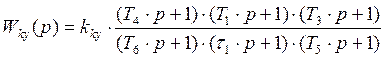
По рис. 2.1.
найдем численные значения неизвестных постоянных времени ![]() ,
, ![]() , и
, и ![]() :
:
![]() ;
; ![]() дек;
дек; ![]() рад/с;
рад/с;
![]() с,
с,
![]() ;
; ![]() дек;
дек; ![]() рад/с;
рад/с;
![]() с,
с,
![]() ;
; ![]() дек;
дек; ![]() рад/с;
рад/с;
![]() с,
с,
Коэффициент передачи регулятора определяем по формуле:
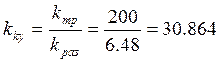
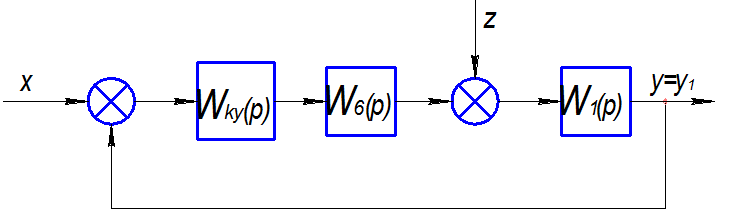
2.4. Структурная схема синтезированной САУ с учетом последовательного корректирующего устройства.
Включаем корректирующий элемент в структурную схему исходной системы.
2.5. Запас устойчивости по фазе скорректированной САУ
Считаем запас устойчивости из передаточной функции
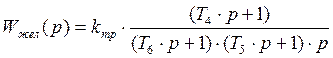
![]() , при A(w)=1
, при A(w)=1
Для форсирующего звена: ![]() ,
,
Для апериодических звеньев: 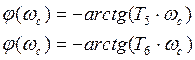 ,
,
Для интегрирующего звена: ![]() .
.
![]()
Запас устойчивости по фазе получился больше данного ![]()
 |
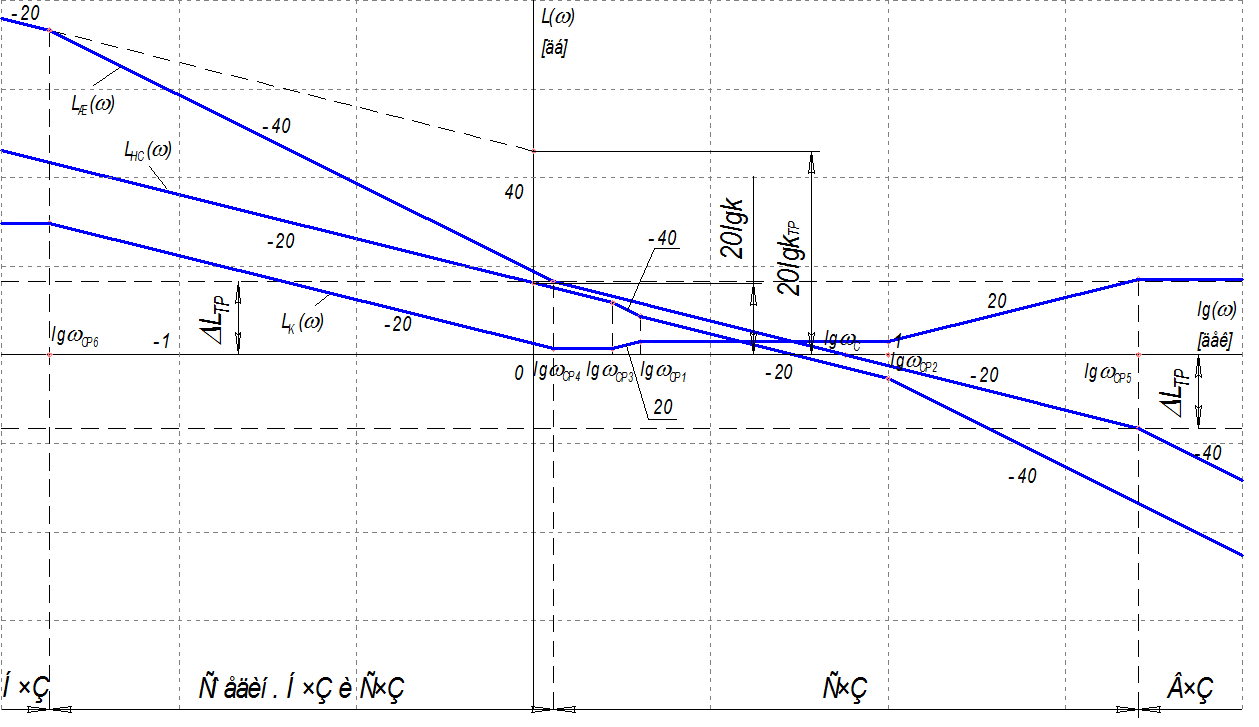
Рис 2.1.
2.6. Проверка результатов синтеза методом цифрового моделирования.
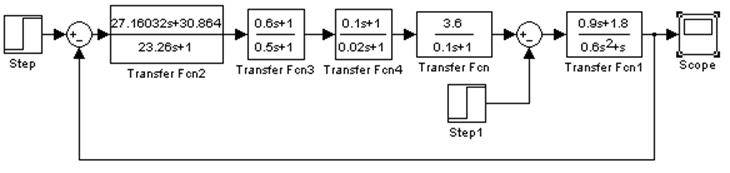
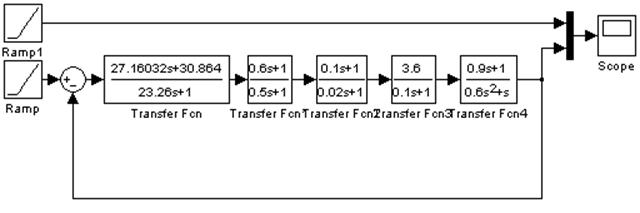
Подставим численные значения параметров в передаточную функцию последовательного корректирующего устройства и построим модель скорректированного устройства в программе «MATLAB 6.5 - SIMULINK»:
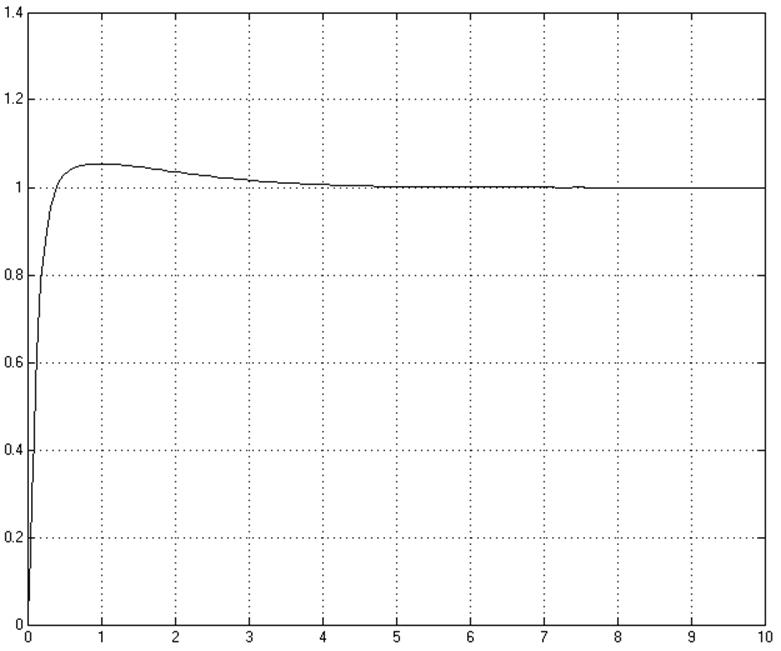
Переходная характеристика скорректированной САУ при единичном ступенчатом задающем воздействии имеет следующий вид:
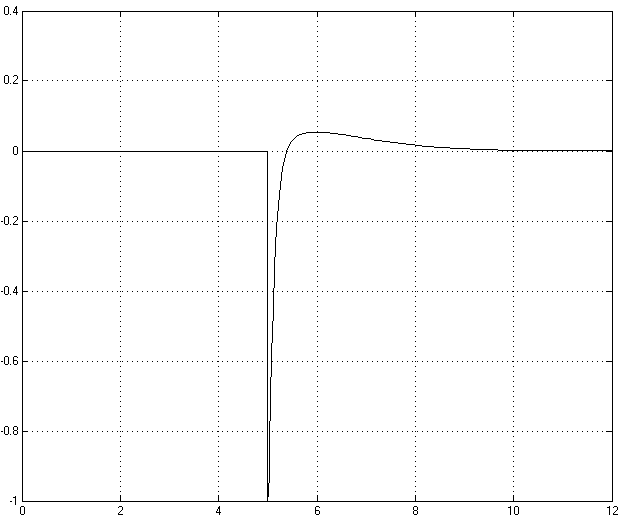
Переходная характеристика скорректированной САУ при единичном ступенчатом возмущающем воздействии имеет следующий вид:
Линейно-возрастающее задающее воздействие на скорректированную САУ
Статическая ошибка
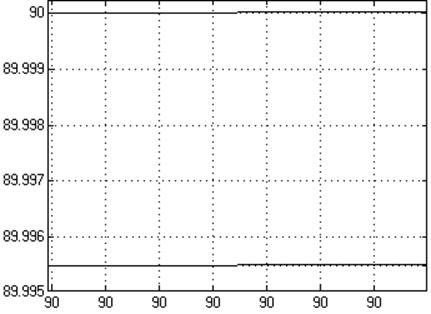
![]()
Переходная характеристика скорректированной САУ при линейно-возрастающем задающем воздействии имеет следующий вид:
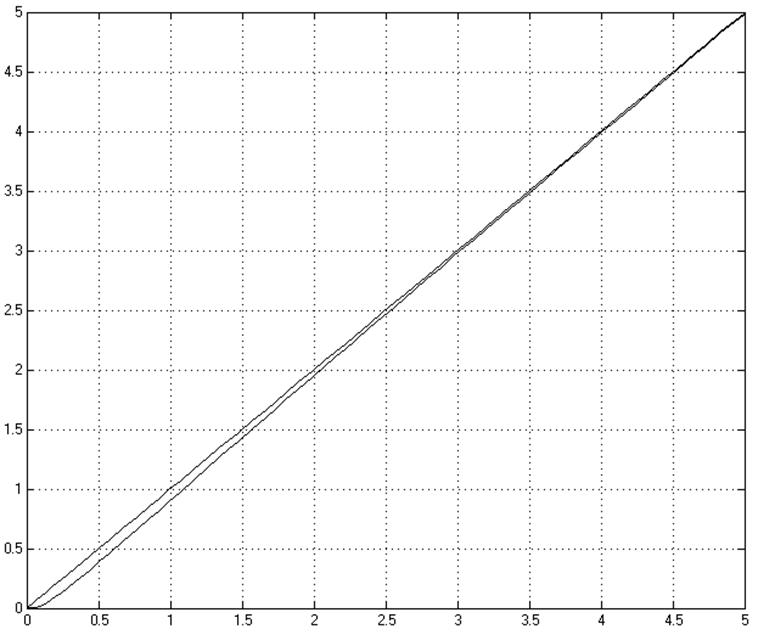
2.7. Вывод
Оценка показателей качества переходного процесса и статической ошибки регулированиия скорректированной САУ при единичном ступенчатом воздействии в соответствии с заданными требованиями:
- время регулирования: ![]() ,
,
- перерегулирование ![]() <
< ![]() ,
,
-
статическая ошибка регулирования ![]() и стремится к нулю, в
отличии от -0.278 при исходной САУ.
и стремится к нулю, в
отличии от -0.278 при исходной САУ.
Оценка статической ошибки регулированиия скорректированной САУ при линейно-возрастающем воздействии в соответствии с заданными требованиями:
- статическая ошибка регулирования ![]() и стремится к нулю.
и стремится к нулю.
Список использованной литературы:
1. Воронов А.А. Теория автоматического управления. Ч. I.Учеб. пособие для вузов. – М.: «Высшая школа», 1977. - 303с.
2. Аносов В.Н., Наумов В.В. Теория автоматического управления Методические указания к лабораторным работам – Новосибирск: НГТУ, 2004. – 62с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.