Анализ модели синтезированной САУ с учетом последовательного корректирующего устройства

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра “Автоматизации производственных процессов в машиностроении”

ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ

“Анализ и синтез линейной системы автоматического управления”

Исходные данные для проектирования:

- номер варианта таблицы уравнений структурной схемы  7;

- номер варианта таблицы параметров объекта управления  9;

- допустимая скоростная ошибка регулирования  0,005;

- максимально – допустимое время регулирования  0,5;

- максимально – допустимое перерегулирование  30%;

Содержание пояснительной записки:

- определение ошибки регулирования по управляющему и возмущающему воздействию в установившемся процессе;

- исследование устойчивости исходного объекта управления;

- определение требуемого коэффициента передачи последовательного корректирующего устройства;

- синтез линейной САУ на основании метода желаемых логарифмических частотных характеристик;

- проверка результатов синтеза методом цифрового моделирования.

Новосибирск 2006 г.

Исходные данные:

Алгебраические уравнения исходной САУ:

Структурная схема:

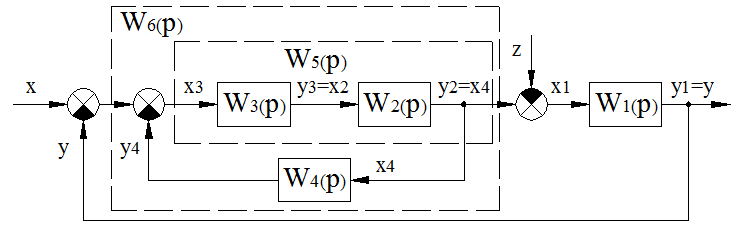
где: x – задающее воздействие; z – возмущающее; xi – входная переменная i – ого звена; yi – выходная переменная i – ого звена; y=y1 – выходная переменная (управляемая) переменная САУ.

Параметры динамических звеньев исходной САУ:

                  

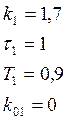
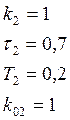
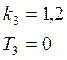
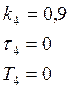
1. Система обыкновенных дифференциальных уравнений, описывающая динамику исходной САУ:

                    

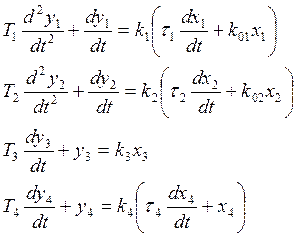
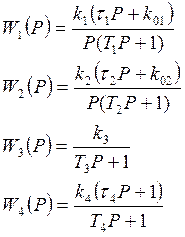
2. Желаемые показатели качества переходных процессов и статическая точность регулирования:

- допустимая скоростная ошибка регулирования:

- максимально – допустимое время регулирования:

- максимально – допустимое перерегулирование:

                                             Анализ линейной САУ:

1. Схема исходной нескорректированной САУ:

2. Дифференциальные уравнения с учетам численных значений:

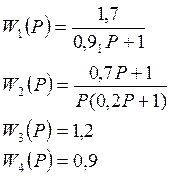
3. Структурная схема в стандартном виде:

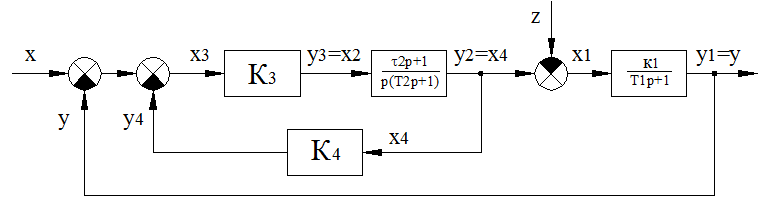
4. Преобразуем систему в однородную:

;

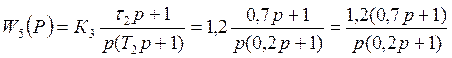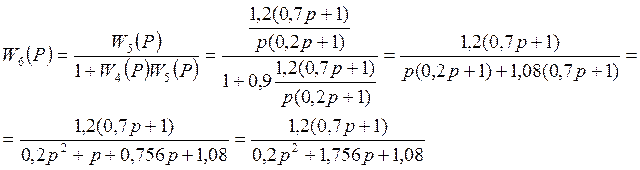
Сократим на 1,08:

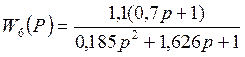 , где

1,1 – звено пропорциональности;

(0,7p+1) – форсирующее звено;

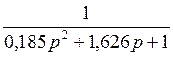   – колебательное звено.

Колебательное звено в общем виде:

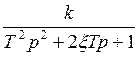; найдем  для нашего случая:

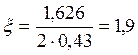, так как >1, то заменим колебательное звено двумя

апериодическими:

D=1,9

;

;

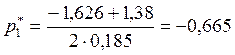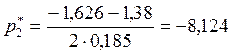
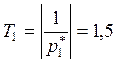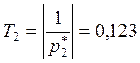
Получим:

.

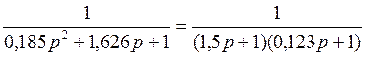Одноконтурная структурная схема:

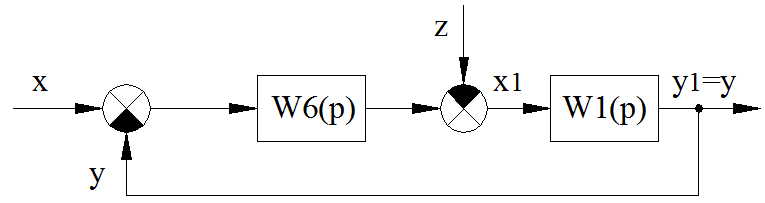
Передаточная функция разомкнутой САУ:

 

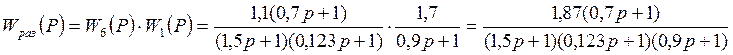
где   

5. Передаточная функция замкнутой САУ по задающему x воздействию:

 

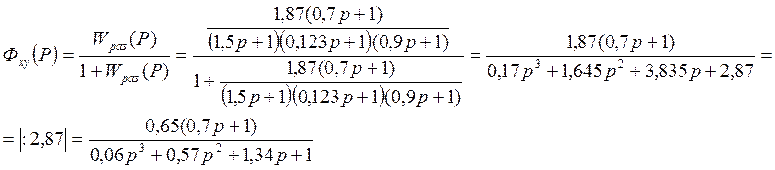
По возмущающему z воздействию:

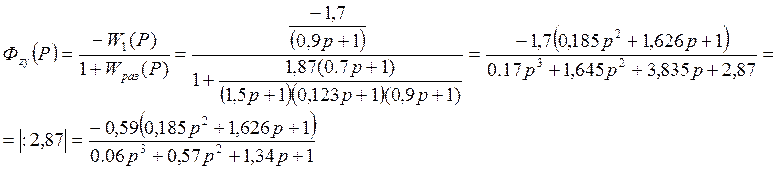
Уравнение замкнутой системы в дифференциальной форме y=F(x;y) имеет вид:

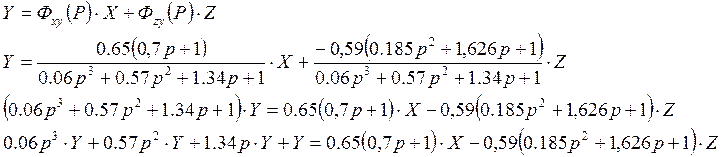
Запишем уравнения в дифференциальном виде:

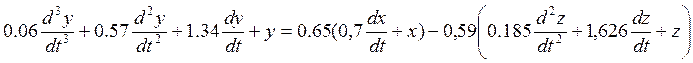
Определим статическую ошибку в случае приложения единичного ступенчатого сигнала:

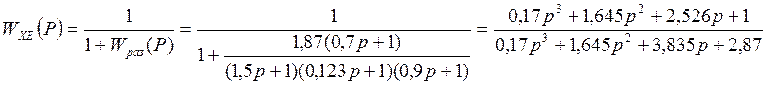
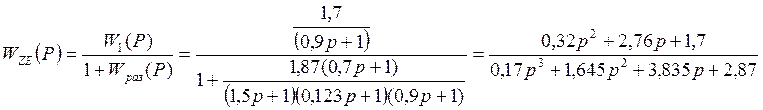
Найдём статическую ошибку:

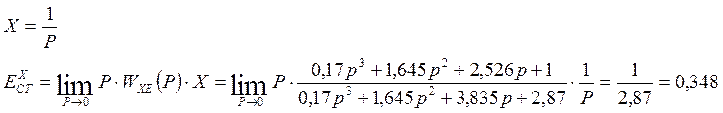
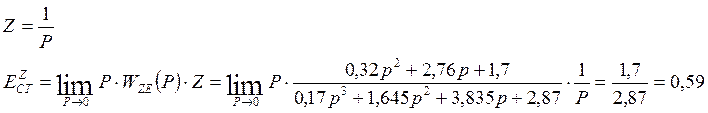
6. При помощи алгебраического критерия устойчивости Гурвица проверим условие устойчивости нескорректированной САУ:

Подставим численные значения:

1. 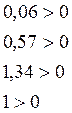, условие выполняется

2. 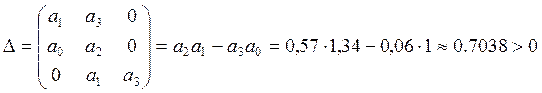, условие выполняется

7. Выполним моделирование с помощью ЭВМ в программе MATLAB. Для моделирования используется исходная структурная схема, в которой все элементы представлены типовыми звеньями.

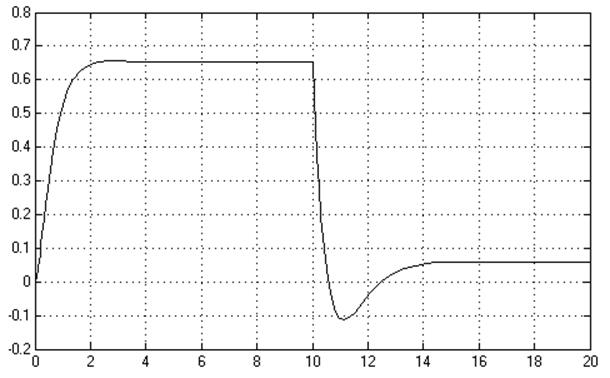
Рис.1. Модель исходной системы.

Проанализируем систему:

1. ;

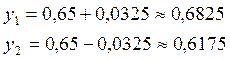
2. Определим статическую ошибку.

Для ступенчатого сигнала по x:

Для ступенчатого сигнала по возмущению:

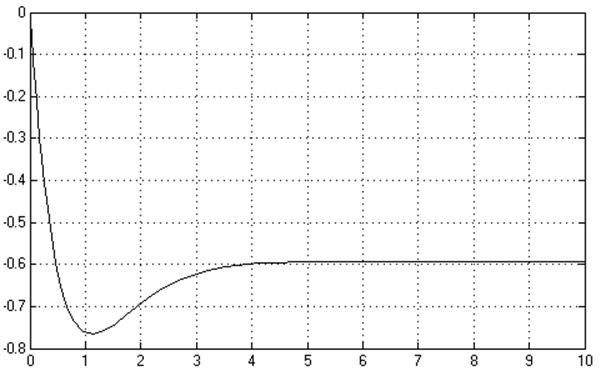
Рис.2. Подача ступенчатого сигнала по возмущению.

Вывод: Переходные процессы получаем как реакцию системы на единичные ступенчатые задающее и возмущающее воздействия при нулевых начальных значениях выходных величин всех типовых звеньев. На рис.1 и 2 представлены графики переходных процессов при подаче единичного ступенчатого сигнала по управлению и возмущению

Время переходного процесса ;

Перерегулирование отсутствует.

Статическая ошибка при подаче единичного ступенчатого сигнала по задающему воздействию равна , что соответствует результатам вычисления. Статическая ошибка при подаче единичного ступенчатого сигнала по возмущающему воздействию равна , что также соответствует результатам вычисления.

Синтез последовательного корректирующего устройства

на основании метода желаемой ЛАЧХ.

1. Изображаем асимптотическую ЛАЧХ нескорректированной системы Lнс(ω) с использованием логарифмического масштаба ω. Продольную ось L(ω) проводим через единичную частоту ω=1. (Рис.3. линия Lнс(ω))

Определим характеристики для соответствующих звеньев:

пропорциональное звено: ;

форсирующее звено: ;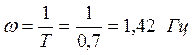

апериодическое звено: ;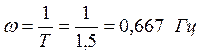

апериодическое звено: ;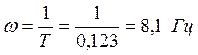

апериодическое звено: .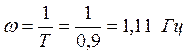

2. Строим желаемую ЛАЧХ астатической скорректированной САУ Lжел(ω), обеспечивающей заданные показатели качества переходных процессов s%=30%, tр=0,5 и требуемую скоростную ошибку Δyдоп(∞)=0,005, которая состоит из низкочастотной, среднечастотной и высокочастотной области.

Построение желаемой ЛАЧХ:

- наклон НЧ области желаемой ЛАЧХ принимаем равным -20дБ/дек. Требуемый разомкнутый коэффициент передачи kтр скорректированной системы определяем как:

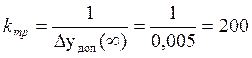
- по номограммам, задавшысь требуемыми значениями перерегулирования