этого в каждой точке времени измеряют значение амплитуды сигнала и записывают в виде чисел. Такое кодирование аналогового сигнала в цифровую форму называется его оцифровкой или аналогово-цифровым преобразованием (АЦП).
Однако в этом методе есть свои недостатки, так как значения амплитуды сигнала мы не можем записывать с бесконечной точностью, и вынуждены их округлять. Таким образом, оцифровка сигнала включает в себя два процесса - процесс дискретизации (осуществление выборки) и процесс квантования. Процесс дискретизации - это процесс получения значений величин преобразуемого сигнала в определенные промежутки времени.
Квантование - процесс замены реальных значений сигнала приближенными с определенной точностью (рис. 1).
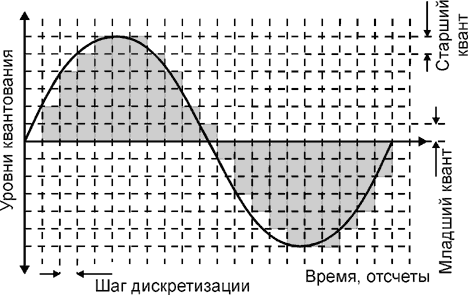
Выбирая частоту дискретизации (sample rate) fd (или обратную ей величина шаг времени отсчета dt), мы получим дискретные моменты времени ti (t0 + i*dt) в которые будут производиться замеры функции и вычисляются отсчетные значения Ai(t). Такие наборы пар (ti, Ai(t)) называются дискретами или сэмплами. Набор дискретов и представляет собой оцифрованный из канала звук.
При преобразовании звукового сигнала необходимо находить компромисс между качеством и занимаемым оцифрованным сигналом объемом.
Для оцифровки аналогового сигнала большое значение имеет критерий Найквиста, который указывает минимальную частоту дискретизации. Это математическая теорема рассматривает функции с финитным спектром, т.е. у которых частотные составляющие выше некоторой частоты (Fmax) равны нулю. Для звуковых сигналов Fmax = 20000 Гц. Теорема утверждает, что для получения точных отсчетных значений аналогового сигнала, частоту дискретизации fd надо брать как минимум в 2 раз выше Fmax.
Этот критерий является следствием из теоремы Котельникова, которая в свою очередь представляет собой частный случай разложения функции в ряд Фурье. В соответствии с теорией Фурье, звуковую волну можно представить в виде спектра входящих в нее частот.
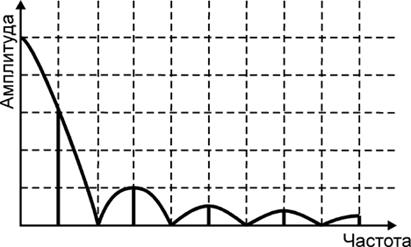
Частотные составляющие спектра - это синусоидальные колебания, каждое из которых имеет свою собственную амплитуду и частоту. Любое, даже самое сложное по форме колебание (например, человеческий голос), можно представить суммой простейших синусоидальных колебании определенных частот и амплитуд. Сгенерировав различные колебания и наложив их друг на друга (смешав), можно получить различные звуки.
Однако при выполнении оцифровки звука появляются различные шумы и искажения, связанные с дискретностью информации об амплитуде оригинального сигнала и погрешностью формирования точек отсчета. Эти погрешности приводят к ощущению дрожания и искажению при проигрывании
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.