Тема: Решение систем линейных алгебраических уравнений (СЛАУ) итерационными методами.
Цель: Научиться решать системы линейных алгебраических уравнений с применением ЭВМ итерационными методами
Задание:
1. Составить программу ЭВМ для решения СЛАУ методом соответственно варианту.
2. Решить две СЛАУ, матрица и правые части, которых были заданы в лабораторной работе №1 (создаются программами lr1K2.exe и lr1bK2.exe соответственно варианту).
3. Оценить погрешность значений неизвестных.
Метод решения СЛАУ для вариантов:
3,6,9,12,15,18,21,24,27,30 - спрягающих градиентов.
Теоретическая часть работы
Методика решения:
Итерационные методы решения СЛАУ
Рассмотренные методы решения СЛАУ путем сводки к треугольному виду – метод последовательного исключения неизвестных Гаусса, рекуррентными формулами схемы Халецкого и квадратного корня – принадлежат к классу так называемых “точных методов”. К сожалению, характеристика “точный” в данном случае не гарантирует получения точного решения, а означает, что метод позволяет за определенное число математических операций получить точное решение при условии отсутствия погрешности вычислений. На практике, при использовании в вычислениях на ЭВМ представления вещественных чисел с фиксированным количеством разрядов всегда собравшиеся погрешность округления а отсюда и погрешность вычислений. С увеличением размеров системы растет количество математических операций нужных для ее решения и как следствие погрешность вычислений. В случае так называемых плохо обусловленных систем погрешность решения полученного за “точными” методами может оказаться неприемлемой.
Разработанные итерационные методы решения СЛАУ, которые позволяют последовательно уточнять решение, начиная с некоторого приближения. Для этих методов также существуют границы точности, которую можно достичь при их применении, но они могут оказаться роботоспроможними, когда “точные” уже не работают. Кроме того, они, в определенных случаях, требуют меньшей памяти ЭВМ.
Превратим СЛАУ![]() к эквивалентной системе:
к эквивалентной системе:
![]() (1)
(1)
Выберем начальное
приближение решения ![]() и используем (1) как
итерационную формулу:
и используем (1) как
итерационную формулу:
![]() (2)
(2)
С помощью которой получим последовательность приближений
решения ![]() ,
,![]()
Если эта последовательность совпадает![]() ,
то
,
то ![]() является точным решением (1) –
является точным решением (1) –![]() и значит начальной системы.
и значит начальной системы.
Варианты эквивалентных превращений системы:
![]() ,
,
![]() .
.
где ![]() - произвольная матрица, а
- произвольная матрица, а ![]() – скаляр, от значений
которых зависит сходимость метода.
– скаляр, от значений
которых зависит сходимость метода.
Условия сходимости метода итераций:
![]()
(![]() ,
, ![]() )
)
То
есть последовательность приближений решения будет совпадать, если при умножении
на матрицу![]() в (1) модуль вектора уменьшается (другими
словами матрица
в (1) модуль вектора уменьшается (другими
словами матрица ![]() является оператором, что
сжимает):
является оператором, что
сжимает): ![]() . Условие сходимости может быть определено
через норму матрицы.
. Условие сходимости может быть определено
через норму матрицы.
Норму матрицы можно определить следующим образом:
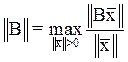 ,
,
где ![]() является символом нормы. То есть
норма матрицы равняется максимальному значению коэффициента увеличения нормы
векторов от умножения на эту матрицу. В зависимости от определения нормы векторов
им будут отвечать такие нормы матриц.
является символом нормы. То есть
норма матрицы равняется максимальному значению коэффициента увеличения нормы
векторов от умножения на эту матрицу. В зависимости от определения нормы векторов
им будут отвечать такие нормы матриц.
1. Норма вектора определяется как его модуль:
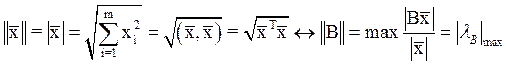 (3)
(3)
где ![]() наибольшее за модулем собственное число
матрицы. Такая норма матрицы зовется спектральной.
наибольшее за модулем собственное число
матрицы. Такая норма матрицы зовется спектральной.
2. Норма вектора определяется как его наибольшая за модулем координата:
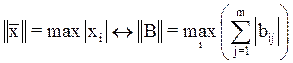 , (4)
, (4)
то есть норма матрицы равняется максимальной из сумм абсолютных значений элементов ее строк.
3. Норма вектора определяется как грусть абсолютных значений его координат:
 , (5)
, (5)
то есть норма матрицы равняется максимальной из сумм абсолютных значений элементов ее столбцов.
Условием сходимости интеграционного процесса вычисляется по
формуле (2) будет ![]() , где норма вычисляется за одной
из формул –(3), (4), или (5).
, где норма вычисляется за одной
из формул –(3), (4), или (5).
Метод Зейделя основан на следующем превращении системе уравнений:
![]()
![]()
![]() ,
,
где: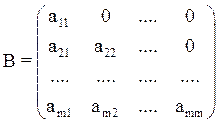 ;
; 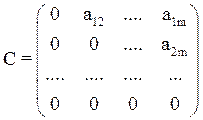 ; и
; и ![]() .
.
Соответствующая итерационная формула будет такой:
![]() ,
,
но, чтобы не вычислять обратную матрицу ![]() , можно воспользоваться эквивалентной
формулой:
, можно воспользоваться эквивалентной
формулой:
![]() ,
,
Решая в каждой итерации систему с треугольной матрицей.
Алгоритм метода Зейделя:
n:=0; ![]() ;
;
цикл
вычислить ![]() с
с
![]() ;
;
n:=n+1;
пока ![]() или n > nmax
или n > nmax
Связь задачи решения СЛАУ с симметричной положительный определенной матрицей и минимизации квадратичной формы
Матрица есть симметрично,
если и положительный определенной, если ![]() при будь которых
при будь которых ![]() . хотя СЛАУ с
такой матрицей является случаем части, они встречают часто при решении
прикладных задач. для СЛАУ с положительный определенной матрицей развязок
системы одновременно дает минимум квадратичной формы:
. хотя СЛАУ с
такой матрицей является случаем части, они встречают часто при решении
прикладных задач. для СЛАУ с положительный определенной матрицей развязок
системы одновременно дает минимум квадратичной формы:
![]()
и наоборот вектор, что минимизирует эту форму является решением системы. это дало основу для разработки так называемых градиентных методов которые являются эффективными при решении больших систем.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.