Решение систем линейных алгебраических уравнений итерационными методами, страница 2

метод самого быстрого градиентного спуска метод самого быстрого градиентного спуска построен на поиске следующего приближения за направлением градиенту квадратичной формы:

,

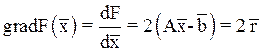так что:

,

при чем  определяется из условия минимизации квадратичной формы на каждой итерации:

.

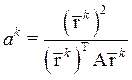Алгоритм метода самого быстрого градиентного спуска:

k:=0;    ;

цикл

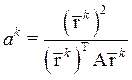;       ;        k:=k+1;

пока      или   к > kmax

Метод спрягающих градиентов

За этим методом следующее приближение находится на так называемых

А – ортогональных направлениях:

;    ,

при чем эти направления избираются в плоскостях перпендикулярных поверхностям уровня квадратичной формы:

.

Коэффициент  вычисляется из условия А – ортогональной:

,

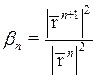а   – минимуму квадратичной формы:

.

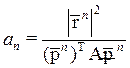Алгоритм метода спрягающих градиентов: 

;   ;    ;    ;

цикл

;    ;  ;   ;

;  

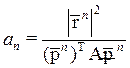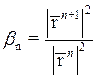пока      или   n > nmax

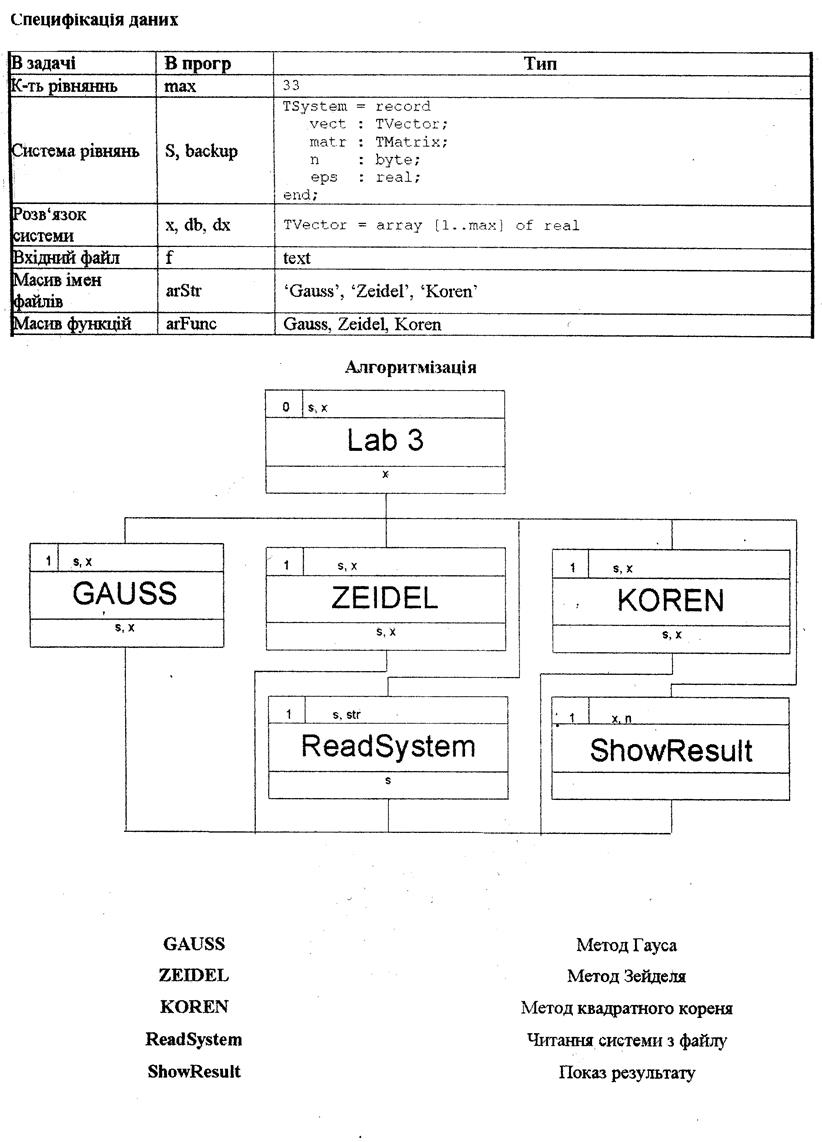
Блок-схема программы:

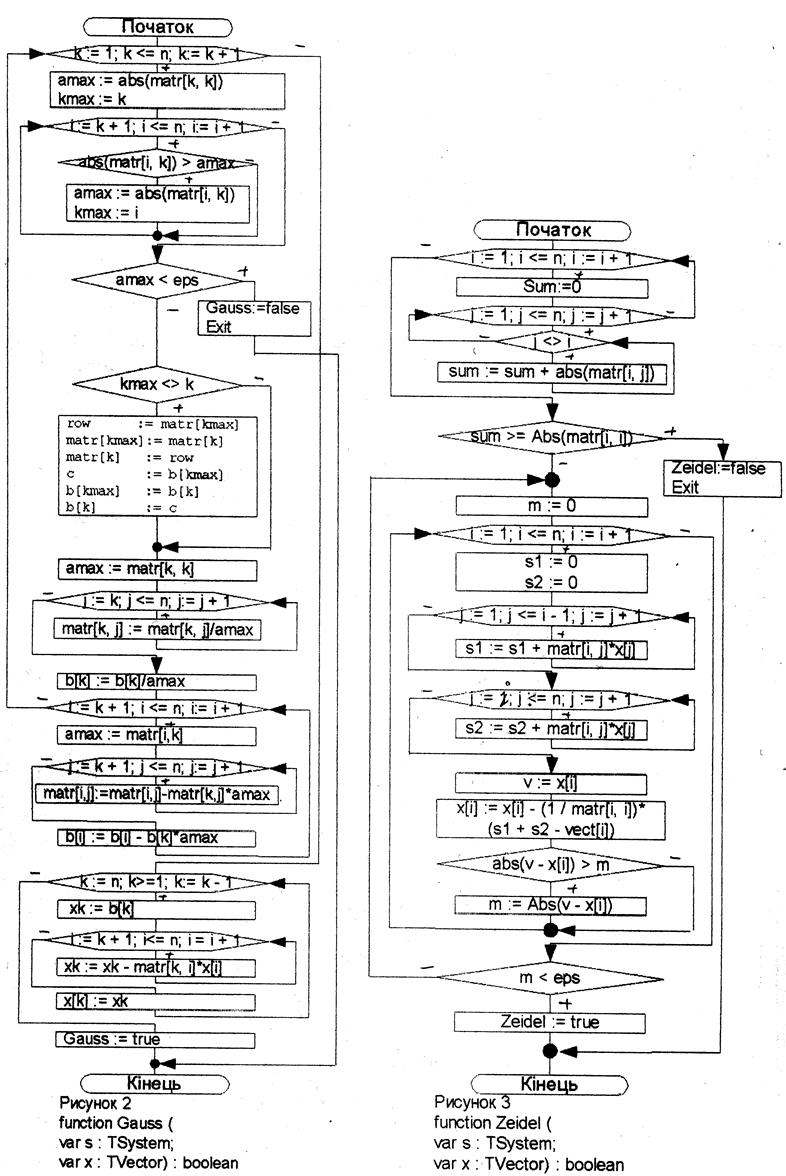
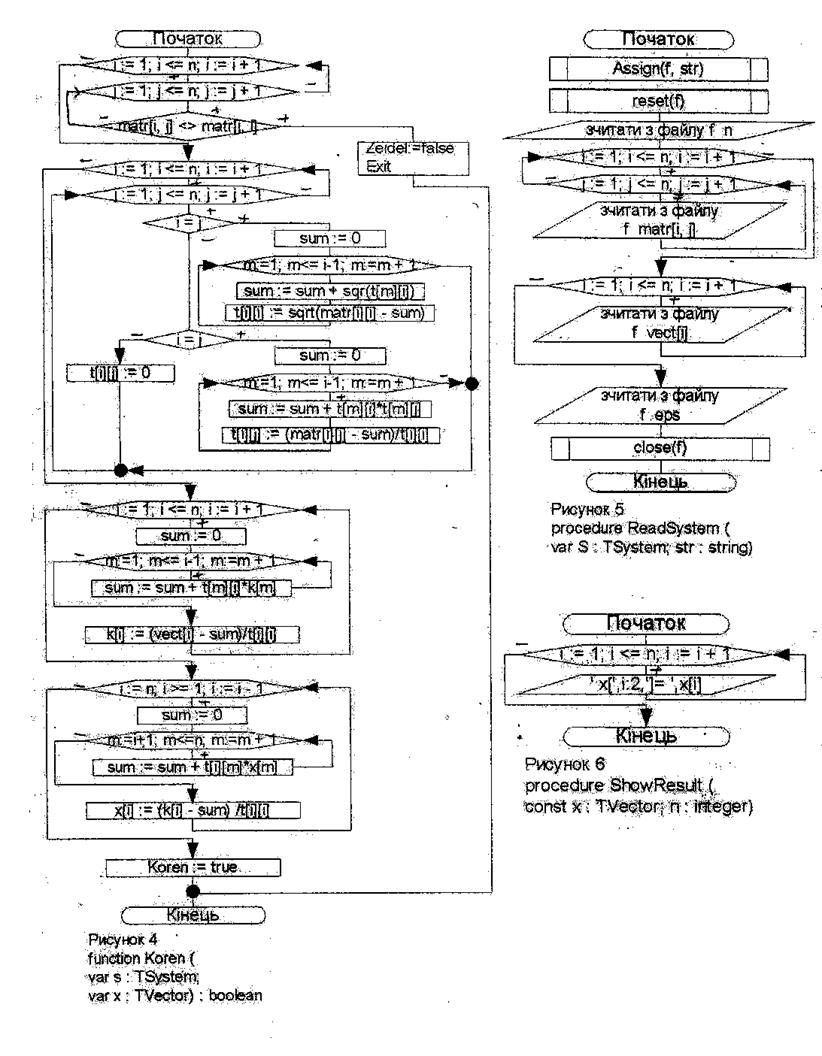
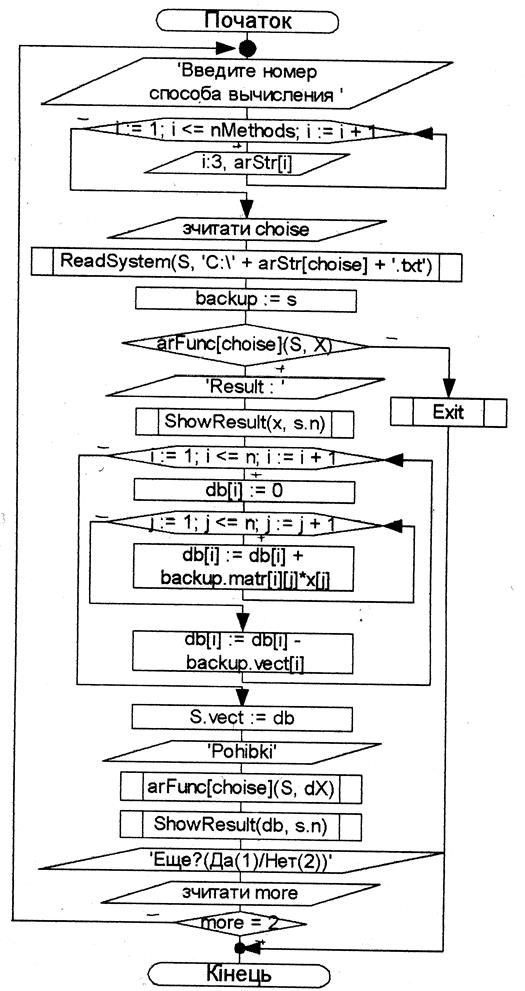
Текст программы:

Текст основной программы:

program SLAU;

uses crt, Un_Vvod, U_Gauss, U_Zeidel, U_Iter, U_Koren, U_Prog ;

var i,j,n,kol,status:integer;

    eps,s:real;  A:matrix; B,x:vector;

    fr:text;     key:char; fnr:string[15];

procedure Menu;

begin

     clrscr;

     writeln('Menu:');            writeln('1. Gauss');

     writeln('2. Iteraction');    writeln('3. Zeidel');

     writeln('4. Kvadr koren');   writeln('5. Progonka');

     writeln('6. Exit programm'); writeln;    write('Enter your chois: ');

     key:=readkey;

end;

procedure FillOut;

begin

       writeln;

       writeln('Input output filename: ');

       readln(fnr);

       assign(fr,fnr);

       rewrite(fr);

       writeln(fr,'Matrix A');

       for i:=1 to n do

       begin

            for j:=1 to n do write(fr,a[i,j]:7:1);

            writeln(fr);

       end;

       writeln(fr,'Your chois nm=',key);

       for i:=1 to n do writeln(fr,'  result x[',i,']=',

                     x[i]:10:5);

       close(fr);

       writeln('Results in file: ',fnr);

       readln;

end;

begin

     clrscr;

     Vvod(n,eps,A,B);

     repeat

       status:=0;

       Menu;

       case key of

         '1':Gauss (A,B,n,eps,x,status);

         '2':Iter(A,B,n,eps,x,status);

         '3':Zeidel (A,B,n,eps,x,status);

         '4':Koren(A,B,n,eps,x,status);

         '5':Run_Prog(A,B,n,eps,x,status);

       end;

       for i:=1 to n do

       begin

            s:=0;

            for j:=1 to n do s:=s+a[i,j]*x[j];

            e[i]:=s-b[i]

       end;

       writeln;

       for i:=1 to n do

         writeln('Невязки: E[',i,']= ',E[i]:10:5);

       if(status=1) then FillOut;

       until(key='6');

end.

Текстмодуля (U_gauss):

unit u_Gauss;

interface

uses UN_VVOD;

procedure Gauss(A:matrix; B:vector; n:integer; eps:real;

                          var x:vector; var stat:integer);

implementation

procedure gauss;

 var i,j,k,l:integer;

     r,SUM,max:real;

 begin

  for k:=1 to n do

   begin

   max:=abs(a[k,k]);

   l:=k;

   for i:=1+k to n do

   if abs(a[i,k])>max then

    begin

     max:=abs(a[i,k]);

     l:=i;

    end;

   if max<eps then begin writeln('Матрица системы вырождена '); halt end;

   if l<>k then

  begin

  for j:=k to n do

   begin

     R:=a[k,j]; a[k,j]:=a[l,j]; a[l,j]:=R

   end;

       r:=b[k]; b[k]:=b[l]; b[l]:=R

   end;

   for j:=k+1 to n do

       a[k,j]:=a[k,j]/a[k,k];

   b[k]:=b[k]/a[k,k];

       a[k,k]:=1;

   for i:=k+1 to n do

    begin

    for j:=k+1 to n do

    a[i,j]:=a[i,j]-a[k,j]*a[i,k];

    b[i]:=b[i]-b[k]*a[i,k];

    a[i,k]:=0;

    end;

   end;

   {Обратный ход}