-2 ---------
2 2
(1 + x )
Символическое
интегрирование является значительно более сложной задачей, чем
дифференцирование. ToolBox Symbolic Math позволяет работать
как с неопределенными интегралами, так и с определенными. Неопределенные
интегралы от символических функций вычисляются при помощи функции int.
В качестве входных аргументов указываются символическая функция и переменная,
по которой производится интегрирование, например, пусть необходимо вычислить
неопределенный интеграл ![]() , тогда получим:
, тогда получим:
>> syms x
>> f=sym('exp(2*x)');
>> I=int(f,x)
>> pretty(I)
1/2 exp(2 x)
Разумеется, что функция Int не позволяет получить неопределенный интеграл от произвольной функции.
Для нахождения определенного интеграла в символическом виде следует задать нижний и верхний пределы интегрирования, соответственно, в третьем и четвертом аргументах int:
>> syms x a b
>> f=sym('exp(2*x)');
>> I=int(f,x,a,b);
>> pretty(I)
1/2 exp(2 b) - 1/2 exp(2 a)
Двойные интегралы
вычисляются двукратным применением функции int. Пусть, например, необходимо
вычислить интеграл 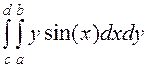 , тогда для его определения необходимо
задать символические переменные a, b, c, d, x, y , подынтегральную
функцию f от xи y и проинтегрировать
сначала по одной переменной, а затем по другой.
, тогда для его определения необходимо
задать символические переменные a, b, c, d, x, y , подынтегральную
функцию f от xи y и проинтегрировать
сначала по одной переменной, а затем по другой.
>> syms a b c d x y
>> f=sym('y*sin(x)');
>> Ix=int(f,x,a,b)
Ix =
-y*cos(b)+y*cos(a)
>> Iy=int(Ix,y,c,d)
Iy =
1/2*(-cos(b)+cos(a))*(d^2-c^2)
>> pretty(Iy)
2 2
1/2 (-cos(b) + cos(a)) (d - c )
>>
Аналогичным образом вычисляются любые кратные интегралы в символическом виде.
3. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
1. Задайте с помощью символических переменных две символические матрицы AиB, размерами 3´3. Определите произведение матриц AиB.
2. Задайте числовую матрицу D, размерами 3´3, содержащую в качестве элементов числа N, N+1, N-1, 0.9N, 2.4, 3.5 и т.д., где N - Ваш номер по списку в журнале группы. Получите из числовой матрицы символическую.
3.
С помощью
символических вычислений определите сумму чисел ![]() где N - Ваш номер по списку
в журнале группы.
где N - Ваш номер по списку
в журнале группы.
4. С помощью символических вычислений определите корень квадратный из числа N.N, с сорока двумя значащими цифрами.
5. Постройте графики символических функций:
![]() -2p < x < 2p;
-2p < x < 2p;
![]() , -10 £ x £ 10; 10 £ y £ 10,
, -10 £ x £ 10; 10 £ y £ 10,
где N - Ваш номер по списку в журнале группы.
6. Полином
![]() , (1)
, (1)
где N - Ваш номер по списку в журнале группы,
с помощью команды pretty отобразите в командном окне, затем преобразуйте его к виду, содержащему степени x с соответствующими коэффициентами.
7. Определите коэффициенты полинома (1) при переменной N.
8. Представьте полином (1) в виде суммы одночленов.
9. Разложите полином (1) на множители.
10. Примените к полиному (1) функцию horner.
11. Представьте число 1000 N+2 N в виде произведения простых чисел.
12. Упростите выражение
![]()
![]()
13.
Получите семь членов ряда Тейлора в окрестности точки нуль для функции ![]()
14.
Определить сумму членов ряда 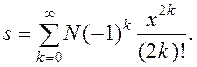
15.
Определите предел ![]()
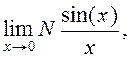 где N - Ваш номер по списку
в журнале группы.
где N - Ваш номер по списку
в журнале группы.
16. Определите пределы 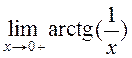 ,
, 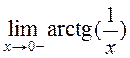 .
.
17. Определите первые три производные от функции
![]()
где N - Ваш номер по списку в журнале группы.
18. Вычислите интеграл 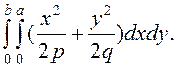
19. Оформите отчет по лабораторной работе.
4. СПИСОК ЛИТЕРАТУРЫ
1. Ануфриев И.Е., Смирнов А.Б., Смирнова Е.Н.Самоучитель MatLab 7. - СПб.: БХВ-Петербург, 2005. - 1104 с.
2. Ануфриев И.Е. Самоучитель MatLab 5.3/6x. - СПб.: БХВ-Петербург, 2004. - 736 с.
3. Кетков Ю. MatLab 6x: программирование численных методов - СПб.: БХВ-Петербург, 2004. - 672 с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.