-------- + ----------------- + ---- + -------
2 A 2 2
(N + x) B C
>> q=subs(f,'x',0)
q =
1+A^2/B^2+1/C^2
>> f3=sym('sin(x)+exp(x)+tan(x)');
>> q1=subs(f3,'x',0)
q1 =
1
2.3. Разложение в ряд Тейлора и определение символических
выражений для сумм
Разложение математических функций в ряд Тейлора позволяет производить функция taylor, например:
>> f=sym('sin(x)');
>> tf=taylor(f);
>> pretty(tf)
3 5
x - 1/6 x + 1/120 x
По умолчанию выводится шесть членов ряда разложения в окрестности точки ноль. Число членов разложения можно задать во втором дополнительном параметре функции taylor. Третий параметр указывает, по какой из переменных следует производить разложение, в том случае, когда символическая функция определена от нескольких переменных. Точка, в окрестности которой проводится разложение, указывается в четвертом входном аргументе функции taylor, например:
>> syms x;
>> f=sym('sin(x)');
>> tf=taylor(f, 5, x, pi/4);
>> pretty(tf)
1/2 1/2 1/2 2
1/2 2 + 1/2 2 (x - 1/4 pi) - 1/4 2 (x - 1/4 pi)
1/2 3 1/2 4
- 1/12 2 (x - 1/4 pi) + 1/48 2 (x - 1/4 pi)
Нахождение символических выражений для сумм, в том числе и бесконечных, позволяет осуществить функция symsum. Обращение к symsum в общем случае предполагает задание четырех аргументов: слагаемого в символической форме, зависящего от индекса, самого индекса и верхнего и нижнего предела суммы. Если в слагаемые входит факториал, то следует применить к выражению для факториала функцию sym. Найдите значение бесконечной суммы, являющейся разложением в ряд функции sin(x)
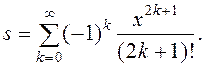
>> syms k x
>> s=symsum((-1)^(k)*x^(2*k+1)/sym('(2*k+1)!'),k,0,inf)
s =
sin(x)
2.4. Определение пределов, дифференцирование и интегрирование
Функция limit находит предел функции в некоторой точке, включая плюс или минус бесконечность. Первым входным аргументом limit является символическое выражение, вторым - переменная, а третьим точка, в которой определяется предел. Пусть, например, требуется вычислить
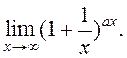
>> syms a x
>> limit((1+1/x)^(x*a),x,Inf)
ans =
exp(a)
Функция limit позволяет находить односторонние пределы. Для нахождения предела справа следует указать четвертый дополнительный аргумент 'right', а слева - 'left'. Найдите решение следующих двух задач
![]()
![]()
>> syms x
>> limit((10+x)^(1/x),x,0, 'left')
ans =
0
>> limit((10+x)^(1/x),x,0, 'right')
ans =
inf
>>
Обратите внимание, что обычный предел в точке нуль не существует:
>> limit((10+x)^(1/x),x,0)
ans =
NaN
Определение
производной через предел позволяет применять limit для дифференцирования
функций. Например, найдем первую производную функции ![]() ,
используя равенство
,
используя равенство
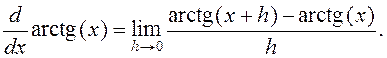
>> syms h x
>> L=limit((atan(x+h)-atan(x))/h, h, 0);
>> pretty(L)
1
------
2
1 + x
Вычисление
производных любого порядка проще производить при помощи функции diff. Символическая запись функции указывается в первом входном аргументе,
переменная, по которой производится дифференцирование - во втором, а порядок
производной - в третьем. Применим diff для вычисления
первой и второй производных функции ![]() :
:
>> P=diff('atan(x)',x,1);
>> pretty(P)
1
------
2
1 + x
>> P=diff('atan(x)',x,2);
>> pretty(P)
x
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.