>> syms a b c d e f g h
>> A=[a b;c d]
A =
[ a, b]
[ c, d]
>> B=[e f; g h]
B =
[ e, f]
[ g, h]
>> C=A*B
C =
[ a*e+b*g, a*f+b*h]
[ c*e+d*g, c*f+d*h]
Функция sym позволяет преобразовывать значения числовых переменных в символические. Введите числовую матрицу A и преобразуйте ее в символическую матрицу B:
>> A=[1.3 -2.1 4.9
6.9 3.7 8.5]
A =
1.3000 -2.1000 4.9000
6.9000 3.7000 8.5000
>> B=sym(A)
B =
[ 13/10, -21/10, 49/10]
[ 69/10, 37/10, 17/2]
При переходе от
числовых выражений к символическим используется запись числа в виде
рациональной дроби. Использование рациональных дробей при выполнении
символических вычислений позволяет всегда получать точный результат, не
содержащий погрешности округления. Убедиться в этом можно на следующем простом
примере. Установите формат long для отображения
максимально возможного числа значащих цифр для значений числовых переменных и
найдите сумму чисел ![]() и
и ![]() .
.
>> format long
>> 1.0e10+1.0e-10
ans =
1.000000000000000e+010
Теперь преобразуйте числа в символические переменные и снова вычислите сумму:
>> large=sym(1.0e10);
>> small=sym(1.0e-10);
>> s=large+small
s =
100000000000000000001/10000000000
Рациональная дробь является точным значением суммы. Понятно, что символические вычисления требуют больших временных затрат по сравнению с обычными.
Вычисление символических выражений производится с помощью функции vpa, например:
>> c=sym('sqrt(2)');
>> cn=vpa(c)
cn =
1.4142135623730950488016887242097
По умолчанию сохраняется тридцать две значащие цифры. Второй входной параметр функции vpa позволяет задавать вычисления с заданным числом разрядов, например, с 50 разрядами:
>> cn=vpa(c,50)
cn =
1.4142135623730950488016887242096980785696718753769
Выходное значение функции vpa является символической переменной, но его можно использовать в обычных вычислениях, например:
>> cn=vpa(c,50)
cn =
1.4142135623730950488016887242096980785696718753769
>> cn+2
ans =
3.4142135623730950488016887242096980785696718753769
>> cn*2
ans =
2.8284271247461900976033774484193961571393437507538
Результат арифметических операций в этих случаях получается в символических переменных. Для перевода символических переменных в числовые, т.е. переменные типа double array, используется функция double:
>> cnd=double(cn)
cnd =
1.41421356237310
Визуализация символических функций одной переменной осуществляется при помощи ezplot. Самый простой вариант использования ezplot состоит в указании символической функции в качестве единственного входного аргумента, при этом в графическое окно выводится график функции на отрезке [-2p, 2p]. Например:
>> f=sym('x*sin(x^2)^3');
>> ezplot(f)
Обратите внимание (рис. 1), что автоматически создается соответствующий заголовок. Вторым аргументом может быть задан вектор с границами отрезка, на котором требуется построить график функции:
>> ezplot(f,[-9 7])
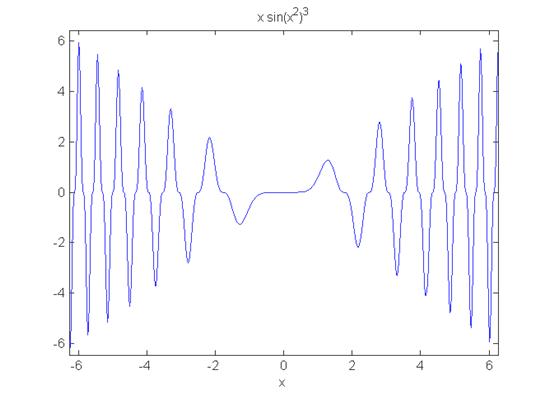
Рис.1. График символической функции
Функция ezplot имеет некоторые отличия от своего аналога - функции fplot, применяемой к числовым функциям. В частности, возможно указание символической функции, зависящей от двух аргументов:
>> z=sym('x^2+a^3');
>> ezplot(z,[-2 1 -3 4])
Пределы изменения аргументов определяются их названиями. Первые два числа соответствуют первому по алфавиту аргументу, а последние - второму. В рассматриваемом примере a изменяется от -2 до 1, а x изменяется от -3 до 4. В графическое окно выводится линия, удовлетворяющая выражению x^2+a^3=0.
ToolBox Symbolic Math предоставляет пользователю целый набор средств для визуализации символических функций [1, 2].
2.2. Упрощение и преобразование выражений
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.