


Міністерство освіти та науки України
Національний технічний університет “ХПІ”
Кафедра обчислювальної техніки та програмування
ЗВІТ
про виконання лабораторної роботи №7
з навчальної дисципліни “Методика алгоритмів та прийняття рішень”.
Тема роботи:
“ Рішення задач прийняття рішення з векторними критеріями ”
Виконав: студ. гр. КІТ-14Б
Богачов О. С.
Перевірили: Заковоротний О.Ю.
Хавіна І.П.
Харків 2008
Тема: Рішення задач прийняття рішення з векторними критеріями.
Мета: Придбання і закріплення знань, отримання практичних навиків рішення задач прийняття рішення з векторними критеріями.
Хід роботи:
Формалізуємо ситуацію обрання танку у вигляді задачі прийняття рішення з векторним критерієм:
Нехай існує 7 моделей танків, умовно позначених літерами A, B, C, D, E, F, G та 5 критеріїв:
![]() − ціна, у.о.
− ціна, у.о.
![]() − товщина лобової броні, мм.
− товщина лобової броні, мм.
![]() − об`єм бака, см³.
− об`єм бака, см³.
![]() − боєзапас.
− боєзапас.
![]() − максимальна швидкість, км/г
− максимальна швидкість, км/г
Таблиця1.
|
|
|
|
|
|
|
|
A |
80000 |
20 |
17.2 |
238 |
80 |
|
B |
55000 |
21 |
17.0 |
180 |
65 |
|
C |
37000 |
19 |
16.2 |
150 |
60 |
|
D |
43000 |
25 |
17.3 |
182 |
65 |
|
E |
23000 |
18 |
14.1 |
140 |
60 |
|
F |
18000 |
17 |
15.0 |
135 |
55 |
|
G |
10000 |
15 |
11.2 |
120 |
55 |
Правило абсолютної переваги.
Це вирішальне правило припускає, що кращий об'єкт не гірше іншого об'єкта по жодному компоненту векторного критерію.
![]() ,
, ![]() (1)
(1)
Критерії
![]() та
та ![]() не
відповідають припущенню про те, що чим більше значення критерію тим він краще.
Тому необхідно перетворити вихідну задачу:
не
відповідають припущенню про те, що чим більше значення критерію тим він краще.
Тому необхідно перетворити вихідну задачу:
![]() *
= 80000 -
*
= 80000 - ![]() ,
,
Таблиця2.
|
|
|
|
|
|
|
|
A |
0 |
20 |
17.2 |
238 |
80 |
|
B |
25000 |
21 |
17.0 |
180 |
65 |
|
C |
37000 |
19 |
16.2 |
150 |
60 |
|
D |
43000 |
25 |
17.3 |
182 |
65 |
|
E |
57000 |
18 |
14.1 |
140 |
60 |
|
F |
62000 |
17 |
15.0 |
135 |
55 |
|
G |
70000 |
15 |
11.2 |
120 |
55 |
Перевагу
неможливо встановити ні для яких альтернатив. Один варіант є – альтернатива С
переважніше альтернативи B по
всім критеріям, крім критерію ![]() , тобто об`єм бака, але це не
підходить, бо абсолютної переваги С не добилися. Для інших альтернатив
встановити перевагу за цим правилом взагалі неможливо.
, тобто об`єм бака, але це не
підходить, бо абсолютної переваги С не добилися. Для інших альтернатив
встановити перевагу за цим правилом взагалі неможливо.
Правило більшості.
Альтернатива
![]() переважніше альтернативи
переважніше альтернативи ![]() , якщо співвідношення (1) виконуються не для всіх
показників, а тільки для більшості. Застосовуючи це правило до таблиці 4,
отримаємо: A>B, A>C, A>D, A>E, A>F, A>G, B<C, D>B, B>E, B>F, B>G, D>C, C>E, C>F, C>G, D>E, D>F, D>G, E>F, E>G, F>G.
, якщо співвідношення (1) виконуються не для всіх
показників, а тільки для більшості. Застосовуючи це правило до таблиці 4,
отримаємо: A>B, A>C, A>D, A>E, A>F, A>G, B<C, D>B, B>E, B>F, B>G, D>C, C>E, C>F, C>G, D>E, D>F, D>G, E>F, E>G, F>G.
З цих співвідношень можна зробити висновок, що альтернатива А – найкраща.
Таблиці бальних оцінок.
Замінимо числові показники таблиці 2 на бали:
Таблиця3.
|
|
|
|
|
|
|
|
A |
0 |
6 |
6 |
6 |
4 |
|
B |
1 |
4 |
4 |
4 |
2 |
|
C |
3 |
5 |
3 |
3 |
1 |
|
D |
2 |
3 |
5 |
5 |
3 |
|
E |
4 |
2 |
2 |
0 |
1 |
|
F |
5 |
1 |
1 |
2 |
0 |
|
G |
6 |
0 |
0 |
1 |
0 |
Введемо наступне вирішальне правило: альтернатива X переважніше альтернативи Y, якщо число показників, по яких альтернатива Х перевершує альтернативу Y, більше числа показників, по яких вона уступає альтернативі Y.
При даному вирішальному правилі відношення переваги між альтернативами таблиці 3 визначається таблицею 4:
Таблиця4.
|
A |
B |
C |
D |
E |
F |
G |
|
|
A |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
B |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
C |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
|
D |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
|
E |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
F |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
G |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Як можна побачити з таблиці 4, альтернатива А – найкраща.
Зведення векторного критерію до скалярного.
Для зведення векторного критерію до скалярного можна використати наступну формулу:
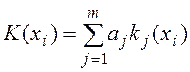
Для розрахунку
необхідно мати коефіцієнти ![]() :
:
Таблиця5.
|
|
|
|
|
|
|
0,1 |
0,1 |
0,3 |
0,2 |
0,3 |
Після проведення розрахунків, отримаємо:
К(х1) = 4,8; К(х2) = 3,1; К(х3) = 4,1; К(х4) = 2,4;
К(х5) = 1,5; К(х6) = 1,3; К(х7) = 0,8.
Отже, альтернатива А – найкраща.
Зведення багатокритеріальної задачі до пошуку екстремуму єдиної цілі в умовах обмежень.
Введемо наступні обмеження:
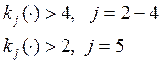
Отже, маємо:
задача 1 (з оптимізацією по критерію ![]() ) {A, D}
) {A, D}
Тепер, після оптимізації по
критерію к1, введемо обмеження ![]()
задача 2 (з оптимізацією по критерію ![]() ) {}
) {}
задача 3 (з оптимізацією по критерію ![]() ) {}
) {}
задача 4 (з оптимізацією по критерію ![]() ) {}
) {}
задача 5 (з оптимізацією по критерію ![]() ) {}
) {}
Таким чином, у результаті рішення шести однокритеріальних задач не вдалося знайти рішення, оптимального до всіх компонентів векторного критерію. Однак число альтернатив, що претендують на оптимальне рішення вихідної задачі, зменшилося до двох (A та D)
Лексикографічний метод рішення багатокритеріальних задач.
Припустимо,
що необхідно придбати танк із великою максимальною швидкістю (ціль найвищого
рангу), великою бронею (ціль другого рангу), великим боєзапасом (ціль третього
рангу), бажано недорогий (ціль четвертого рангу) і з великим об'ємом баку(ціль
нижчого рангу). Із заданої ієрархії цілей випливає, що для визначення кращого
рішення необхідно послідовно використати компоненти векторного критерію ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Застосування
критерію ![]() до даних таблиці 3 дозволяє встановити, що
найкращою альтернативою є альтернатива A, хоч модель
танка і дорога, але в
нього велика броня та велика максимальна швидкість, а це-головне.
до даних таблиці 3 дозволяє встановити, що
найкращою альтернативою є альтернатива A, хоч модель
танка і дорога, але в
нього велика броня та велика максимальна швидкість, а це-головне.
Висновок: в ході лабораторної роботи придбали та закріпили знання, отримали практичні навики рішення задач прийняття рішення з векторними критеріями.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.