Чисельні методи рішення матричних ігор

Міністерство освіти та науки України

Національний технічний університет “ХПІ”

Кафедра обчислювальної техніки та програмування

ЗВІТ

про виконання лабораторної роботи №6

з навчальної дисципліни “Методика алгоритмів та прийняття рішень”.

Тема роботи:

“ Численні методи рішення матричних ігор ”

                                                                              Виконав:  студ. гр. КІТ-14Б

           Богачов О. С.

                                                                          Перевірили: Заковоротний О.Ю.

                                                                                                Хавіна І.П.

Харків 2008

Тема. Чисельні методи рішення матричних ігор

Мета: Придбання й закріплення знань, і одержання практичних навичок роботи при чисельному рішенні матричних ігор.

Індивідуальне завдання:

1. Формалізуйте конфліктну ситуацію у вигляді матричної гри при розмірах матриці не менш 3х3 і відсутності сідлових крапок у чистих стратегіях.

2. Розробіть алгоритм чисельного рішення матричної гри методом послідовного наближення ціни гри. Особливу увагу звернете на умови останова обчислювального процесу.

3. Розробіть програму, що реалізує алгоритм методу послідовного наближення ціни гри.

Хід роботи

Нехай гра задана наступною матрицею

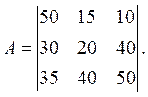
Застосування будь-якого чисельного методу для рішення матричної гри необхідно починати з визначення нижньої чистої ціни гри  a й верхньої чистої ціни гри b.

Отже, і рішення матричної гри необхідно шукати чисельним методом. Припустимо, що в першій партії другий гравець вибрав свою першу стратегію, тоді, якщо перший гравець вибере свою першу стратегію, то він виграє 45, якщо другу   10, якщо третю   15. Зведемо отримані результати в таблицю. З аналізу стовпчика  Сумарний виграш першого гравця по стратегіях  видно, що перша стратегія першого гравця приносить йому найбільший виграш. Тому перший гравець і повинен вибрати свою першу чисту. У цьому випадку, якщо другий гравець вибирає свою першу стратегію, то він програє 45, якщо другу   25, якщо третю   20. Найбільший виграш, що може одержати перший гравець у першій партії, дорівнює 45, оскільки       

Аналогічно, виходить найменший можливий програш другого гравця: 

Знаючи    й ,  , по співвідношенню нескладно обчислити наближене значення ціни гри після першої партії: v = (45 + 20)/2 = 32,5

Оскільки кращий результат у першій партії другому гравцю принесла третя стратегія (програш дорівнює 20), то він її й повинен вибрати в другій партії. У цьому випадку застосування першої стратегії першим гравцем принесе йому виграш в 20 одиниць, підсумовуючи його з виграшем, отриманим за допомогою цієї ж стратегії в першій партії, одержуємо 65. Застосування першим гравцем своєї другої стратегії в поточній партії приносить йому виграш в 40 одиниць і сумарний виграш у двох партіях   50. Аналогічно, застосування третьої стратегії першим гравцем приносить йому виграш у поточній партії в 50 одиниць і сумарний виграш у двох партіях   65. Найбільший виграш у двох партіях першому гравцеві забезпечили відразу дві стратегії: перша й третя. У загальному випадку з погляду  забезпечення стійкості рішення в наступній партії краще вибирати ту стратегію, що була в попередній партії. Тому в другій партії перший гравець застосовує свою першу стратегію. Якщо у відповідь на це другий гравець вибирає свою першу стратегію, то він програє в поточній партії 45 і 90 у двох партіях, якщо вибирає другу стратегію, то програє в другій партії 25 і 50 у двох партіях, якщо вибирає третю стратегію, те відповідно програє 20 і 40. Середній виграш першого гравця у двох партіях дорівнює:   = 65/2 = 32,5; середній програш другого гравця у двох партіях:  =40/2 = 20. Наближене значення ціни гри за результатами двох партій 

Для точного визначення ціни гри в загальному випадку необхідно велика кількість партій, для того щоб нерегулярність примінення стратегій