Информатика и выч. техника \ Методика алгоритмов и принятия решений

Синтез багатокомпонентних критеріїв методом групового обліку аргументів

Страницы работы

4 страницы (Word-файл)
Посмотреть все страницы
Скачать файл

Содержание работы

МІНІСТЕРСТВО ОСВІТИ Й НАУКИ УКРАЇНИ

НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ

«ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ»

Кафедра: «Обчислювальна техніка й програмування»

Звіт

з лабораторної роботи №3

Дисципліна: «Методи та алгоритми прийняття рішень»

                                                                              Виконав:  студ. гр. КІТ-14Б

           Богачов О. С.

                                                                          Перевірили: Заковоротний О.Ю.

                                                                                                Хавіна І.П.

Харків 2008

Лабораторна робота № 3

Тема: Синтез багатокомпонентних критеріїв методом групового обліку аргументів.

Мета роботи: Придбання й закріплення знань, і одержання практичних навичок роботи з методом групового обліку аргументів при синтезі багатокомпонентних критеріїв прийняття рішень.

Індивідуальне завдання:

1.  Задайтеся функцією реалізації розмірами не менш, ніж 8 ´ 7, де вісім альтернатив розглядаються як навчальна безліч M. Віднесіть половину альтернатив до підмножини M1 кращих альтернатив, а що залишилися - до підмножини M2 таким чином, щоб не менш семи однокомпонентних критеріїв не могли правильно класифікувати задана безліч альтернатив (У якості вихідних даних можна використати й дані табл. 1, додавши в неї додаткові рядки або (і) стовпці.)

2.  Синтезуйте, використовуючи Excel і вираження (21) ( (30), на другому ряді селекції не менш 10 ( 15 двухкомпонентних критеріїв й оціните їхню якість роботи.

3.  Синтезуйте, використовуючи Excel, на третьому ряді селекції не менш 5 ( 10 критеріїв й оціните їхню якість роботи. Синтез критеріїв можна припиняти тільки у випадку, коли отриманий хоча б один критерій, що вирішує поставлене завдання.

Хід виконання роботи:

1. Вихідна матриця:

y1

y2

y3

y4

y5

y6

y7

x1

3

7

8

9

10

11

12

x2

2

3

7

8

4

5

12

x3

8

6

5

10

6

7

8

x4

7

5

5

3

10

13

6

x5

4

10

11

12

9

8

7

x6

8

2

12

1

12

11

6

x7

9

3

11

11

10

9

10

x8

5

6

5

11

7

11

10

∑/∑∑

0,1067

0,0974

0,1485

0,1508

0,1578

0,174

0,1647

Розділимо безліч всіх альтернатив на:

§  підмножина кращих альтернатив  

§  підмножина гірших альтернатив

Формули, по яких вироблялися розрахунки:

Ряд селекції 1

Kн

Каи

Кмм

Кs

Кнс

Кссс

Кх

x1

8,5714

12

3

6

2,8571

2,6427

9,6758

x2

5,8571

12

2

8

5,5714

5,4292

6,265

x3

7,1429

10

5

7

4,2857

4,4872

7,8109

x4

7

13

3

7

4,2857

4,4872

8,1433

x5

8,7143

12

4

5

2,7143

2,8492

9,9501

x6

7,4286

12

1

11

4

3,8817

8,5973

x7

9

11

3

7

2,4286

2,3225

9,8352

x8

7,8571

11

5

7

3,5714

3,4733

8,7163

7,8571

12

3

7

3,5714

3,4733

8,7163

2

1

2

2

2

2

2

2

1

2

2

2

2

2

4

2

4

4

4

4

4

де:

Kн - нейтральний критерій

Каи - критерій азартного гравця

Кмм - максиминный критерій

Кs - Критерій Севіджа

Кнс - Нейтральний критерій на жалях

Кссс - Критерій суб'єктивно-середніх жалів

Кх - Критерій Хоменюка

Тому що не один критерій не може правильно ( = 8) розділити вихідна безліч альтернатив, то переходимо до другого етапу селекції.

2.  Формуємо критерії виду:

,

де q-кількість критеріїв після першого етапу селекції.

За допомогою коефіцієнта з можна коректувати вплив кожного критерію на результат оцінки за підсумковим критерієм.

Також, тому що кращими альтернативами по Кs, Кнс і Кссс є даючі найменше значення, а по всім іншим - найбільше, використаємо функції Ks*=10/ Кs, Кнс*= 10/Кнс і Кссс*= 10/Кссс.

Ряд селекції 2

Kн,Кмм

Кн,Кs*

Кн,Кнс*

Кн,Кссс*

Кн,Кх

Кмм,Кs*

Кмм,Кнс*

Kмм,Кссс*

Kмм,Кх

Кs,Кнс*

с

0,6

0,8

0,5

0,5

0,5

0,5

0,5

0,5

0,1

0,2

x1

6,3429

8,0571

7,75

6,1777

9,1236

2,3333

3,25

3,392011

9,008188

4

x2

4,3143

6,2857

6,8974

3,8495

6,061

1,625

1,8974

2,378224

5,838458

3,035897

x3

6,2857

7,1143

6,1667

4,6857

7,4769

3,2143

3,6667

8,81969

7,529783

3,266667

x4

5,4

7

7,6667

4,6143

7,5716

2,2143

2,6667

9,032563

7,628959

3,266667

x5

6,8286

7,9714

7,8421

6,112

9,3322

3

3,8421

7,937787

9,355047

3,947368

x6

4,8571

8,1429

7,25

5,0024

8,013

0,9545

1,75

-9,93541

7,837607

4,2

x7

6,6

8,6

7,5588

6,6528

9,4176

2,2143

3,5588

17,27831

9,151688

4,694118

x8

6,7143

7,6857

6,9

5,3681

8,2867

3,2143

3,9

39,5248

8,344661

3,64

6,3429

7,9714

7,5588

5,3681

8,2867

2,3333

3,5588

8,81969

8,344661

3,947368

2

2

4

2

2

0

0

0

2

2

2

2

4

2

2

0

0

0

2

2

4

4

8

4

4

0

0

0

4

4

Отже, на другому етапі селекції знайдена функція, що правильно розділяє безліч альтернатив М на підмножини:

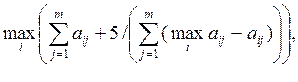= тому подальша селекція не потрібна.

Висновок: Закріпив знання й практичні навички роботи з методом групового обліку аргументів при синтезі багатокомпонентних критеріїв прийняття рішень.

Похожие материалы

Информация о работе

ВУЗ:
Национальный технический университет «Харьковский Политехнический Институт» (ХПИ)
Предмет:
Методика алгоритмов и принятия решений
Тип:
Отчеты по лабораторным работам
Категория:
Информатика и выч. техника (Технические предметы)
Размер файла:
85 Kb
Скачали:
0
Скачать файл