Standard deviation 7,94265 7,96109
Standard error 0,917139 0,796109
Minimum 1,0 1,0
Maximum 30,0 30,0
Range 29,0 29,0
Lower quartile 5,0 5,0
Upper quartile 17,0 17,0
Interquartile range 12,0 12,0
Skewness 0,424386 0,547206
Stnd. skewness 1,50043 2,23396
Kurtosis -0,7101 -0,496218
Stnd. kurtosis -1,25529 -1,0129
Coeff. of variation 66,7076% 65,9576%
Sum 893,0 1207,0
------------------------------------------------------------
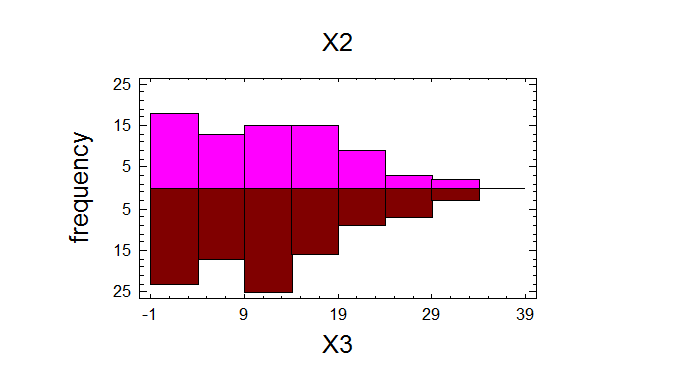
Comparison of Means
-------------------
95,0% confidence interval for mean of X2: 11,9067 +/- 1,82744 [10,0792,13,7341]
95,0% confidence interval for mean of X3: 12,07 +/- 1,57966 [10,4903,13,6497]
95,0% confidence interval for the difference between the means
assuming equal variances: -0,163333 +/- 2,39789 [-2,56122,2,23455]
t test to compare means
Null hypothesis: mean1 = mean2
Alt. hypothesis: mean1 NE mean2
assuming equal variances: t = -0,134445 P-value = 0,893207
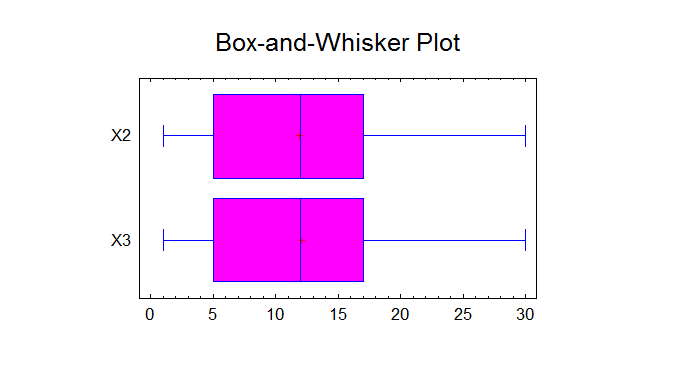
Comparison of Standard Deviations
---------------------------------
X2 X3
------------------------------------------------------------
Standard deviation 7,94265 7,96109
Variance 63,0858 63,3789
Df 74 99
Ratio of Variances = 0,995375
95,0% Confidence Intervals
Standard deviation of X2: [6,84355;9,46566]
Standard deviation of X3: [6,98989;9,2482]
Ratio of Variances: [0,652606;1,53873]
F-test to Compare Standard Deviations
Null hypothesis: sigma1 = sigma2
Alt. hypothesis: sigma1 NE sigma2
F = 0,995375 P-value = 0,991399
Висновок: перевірили статистичні гіпотези для однієї і двох виборок, визначили, що при збільшенні кількості вибірок довірюючий інтервал зменшується, а точність оцінки збільшується.Провели аналіз статистичних гіпотез для усіх комбінацій створених вибірок
Для вибірки 1 та 2:
![]() при
при ![]()
![]()
![]()
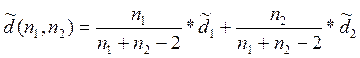 =66.6669
=66.6669
>> s1=69.3718
s1 =
69.3718
>> s2=63.0858;
>> d=(50/(50+75-2))*s1+(75/(50+75-2))*s2
d =
66.6669
Значення статистичного критерія:
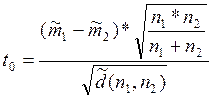 = -1.0510
= -1.0510
>> m1=10.3400;
>> m2=11.9067;
>> t=((m1-m2)*sqrt((50*75)/(50+75)))/sqrt(d)
t =
-1.0510
Для вибірки 1 та 3:
![]() при
при ![]()
![]()
![]()
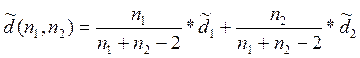 = 66.2600
= 66.2600
>> s1=69.3718;
>> s2=63.3789;
>> d=(50/(50+100-2))*s1+(100/(50+100-2))*s2
d =
66.2600
Значення статистичного критерія:
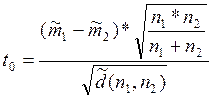 = -1.2270
= -1.2270
>> m1=10.3400;
>> m2=12.0700;
>> t=((m1-m2)*sqrt((50*100)/(50+100)))/sqrt(d)
t =
-1.2270
Для вибірки 2 та 3:
![]() при
при ![]()
![]()
![]()
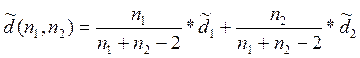 = 63.9845
= 63.9845
>> s1=63.0858;
>> s2=63.3789;
>> d=(75/(75+100-2))*s1+(100/(75+100-2))*s2
d =
63.9845
Значення статистичного критерія:
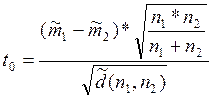 = -0.1336
= -0.1336
>> m1=11.9067;
>> m2=12.07;
>> t=((m1-m2)*sqrt((75*100)/(75+100)))/sqrt(d)
t =
-0.1336
Для вибірки 1:
![]() при
при ![]()
![]()
![]()
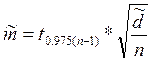 = 2.3742
= 2.3742
>> m1=2.02*sqrt(69.3718/50)
m1 =
2.3742
Для вибірки 2:
![]() при
при ![]()
![]()
![]()
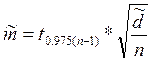 = 1.8352
= 1.8352
>> m2=2.001*sqrt(63.0858/75)
m2 =
1.8352
Для вибірки 3:
![]() при
при ![]()
![]()
![]()
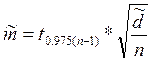 = 1.5800
= 1.5800
>> m3=1.9848*sqrt(63.3689/100)
m3 =
1.5800
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.