Перевірка статистичних гіпотез для однієї та двох вибірок, страница 2

Вибірка№2

Переходимо в процедурний блок  “Describe_Numeric Data-One-Variable_Analysis”,

проводимо розрахунок статистичних даних для першої вибірки і порівнюємо їх з самостійно виконаними розрахунками

Робимо аналітичний розрахунок заданих статистичних характеристик.

Мат. Очікування:

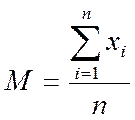=    11.9067

b=[2  22  13  15  26  5  30  9  7  6  8  7  13  12  14  11  16  19  20  3  16  13  12  15  4  3  1  3  3  3  2  5  4  8  10  10  11  16  17  24  21  24  26  28  24  2  13  16  15  19  10  1  2  7  5  17  23  21  20  30  14  12  15  10  9  6  3  2  2 6 1 15 16 19 1]

>> sum(b)

ans =

   893

>> M=ans/75

M =

   11.9067

Дисперсія:

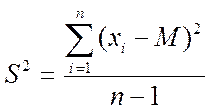= 63.0858

>> b1=(b-M).^2;

>> D=(sum(b1))/74

D =

   63.0858

Стандартне відхилення:

=    7.9427

>> otk=sqrt(D)

otk =

    7.9427

 Стандартна помилка:

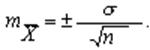=   0.9171

>> osh=otk/(sqrt(75))

osh =

    0.9171

2) Згідно індивідуального завдання перевіряїємо гіпотезу для аналізу однієї вибірки відносно оцінки мат. очікування (варіант№  ) та виконуємо побудову гістограм та графіків „Box and Whisker”

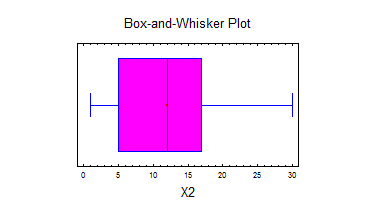
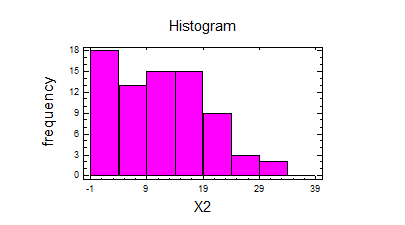
Виконаємо дії по перевірці гіпотез.

Hypothesis Tests for X2

Sample mean = 11,9067

Sample median = 12,0

t-test

------

Null hypothesis: mean = 11,9067

Alternative: less than

Computed t statistic = -0,0000363449

P-Value = 0,499986

Do not reject the null hypothesis for alpha = 0,05.

sign test

---------

Null hypothesis: median = 11,9067

Alternative: less than

Number of values below hypothesized median: 37

Number of values above hypothesized median: 38

Large sample test statistic = 0,0 (continuity correction applied)

P-Value = 0,500003

Do not reject the null hypothesis for alpha = 0,05.

signed rank test

----------------

Null hypothesis: median = 11,9067

Alternative: less than

Average rank of values below hypothesized median: 39,2973

Average rank of values above hypothesized median: 36,7368

Large sample test statistic = 0,150542 (continuity correction applied)

P-Value = 0,440166

Do not reject the null hypothesis for alpha = 0,05.

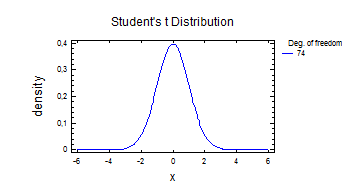
Probability Distributions

Inverse CDF

-----------

Distribution: Student's t

CDF           Dist. 1       Dist. 2       Dist. 3       Dist. 4       Dist. 5

0,975         1,99255      

0,95          1,66571      

The StatAdvisor

---------------

   This pane finds critical values for the Student's t distribution.

You may specify up to 5 five tail areas.  The critical value is

defined as the largest value for the Student's t distribution such

that the probability of not exceeding that value does not exceed the

area specified.  For example, the output indicates that, for the first

distribution specified, 1,99255 is the largest value such that the

probability of not exceeding 1,99255 is less than or equal to 0,975.

Вибірка№3

Переходимо в процедурний блок  “Describe_Numeric Data-One-Variable_Analysis”,

проводимо розрахунок статистичних даних для першої вибірки і порівнюємо їх з самостійно виконаними розрахунками

Робимо аналітичний розрахунок заданих статистичних характеристик.

Мат. Очікування:

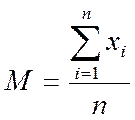=    12.0700

c=[2  4  13  12  11  15  20  21  30  1  4  4  3  5  7  6  8  16  17  18  13  12  14  4  5  9  7  10  10  2  5  4  13  12  12  16  4  30  29  25  29  1  2  14  15  2  6  8  7  4  2  13  15  1  11  17  22  22  24  26  25  21  20  15  16  4  3  18  6  9  11  14  10  1  17  4  2  8  10  6  16  14  5  18  14  12  10  26  21  22  28  30  1  12  16  17  12  10  2  7]

>> sum(c)

ans =

        1207

>> M=ans/100

M = 12.0700

Дисперсія:

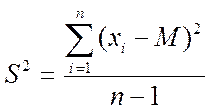= 63.3789

>> c1=(c-M).^2;

>> D=sum(c1)/99

D =

   63.3789

Стандартне відхилення:

=    7.9611

>> otk=sqrt(D)

otk =

    7.9611

 Стандартна помилка:

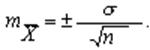=       0.7961

>> osh=otk/(sqrt(100))

osh =

    0.7961

2) Згідно індивідуального завдання перевіряїємо гіпотезу для аналізу однієї вибірки відносно оцінки мат. очікування (варіант№  ) та виконуємо побудову гістограм та графіків „Box and Whisker”