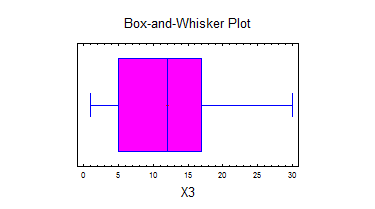
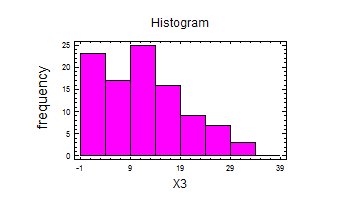
Информатика и выч. техника \ Планирование эксперимента и обработка экспериментальных данных

Перевірка статистичних гіпотез для однієї та двох вибірок, страница 3

Виконаємо дії по перевірці гіпотез.

Hypothesis Tests for X3

Sample mean = 12,07

Sample median = 12,0

t-test

------

Null hypothesis: mean = 12,07

Alternative: less than

Computed t statistic = 0,0

P-Value = 0,5

Do not reject the null hypothesis for alpha = 0,05.

sign test

---------

Null hypothesis: median = 12,07

Alternative: less than

Number of values below hypothesized median: 56

Number of values above hypothesized median: 44

Large sample test statistic = 1,1 (continuity correction applied)

Probability Distributions

Inverse CDF

-----------

Distribution: Student's t

CDF           Dist. 1       Dist. 2       Dist. 3       Dist. 4       Dist. 5

0,975         1,98422      

0,95          1,66039      

The StatAdvisor

---------------

   This pane finds critical values for the Student's t distribution.

You may specify up to 5 five tail areas.  The critical value is

defined as the largest value for the Student's t distribution such

that the probability of not exceeding that value does not exceed the

area specified.  For example, the output indicates that, for the first

distribution specified, 1,98422 is the largest value such that the

probability of not exceeding 1,98422 is less than or equal to 0,975.

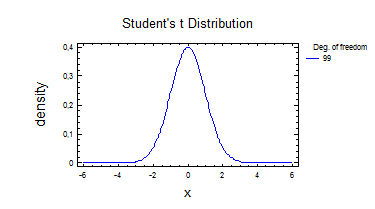
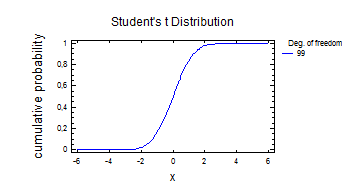
Перевіряємо статичні гіпотези за допомогою пакету Statgraphics для 1 і 2 виборки:

Summary Statistics

                    X1                  X2                  

------------------------------------------------------------

Count               50                  75                 

Average             10,34               11,9067            

Median              8,0                 12,0                

Mode                3,0                                    

Geometric mean      7,2956              8,61484            

Variance            69,3718             63,0858            

Standard deviation  8,32898             7,94265            

Standard error      1,1779              0,917139           

Minimum             1,0                 1,0                

Maximum             30,0                30,0               

Range               29,0                29,0               

Lower quartile      4,0                 5,0                

Upper quartile      15,0                17,0               

Interquartile range 11,0                12,0               

Skewness            1,08537             0,424386           

Stnd. skewness      3,13319             1,50043            

Kurtosis            0,296347            -0,7101            

Stnd. kurtosis      0,427739            -1,25529           

Coeff. of variation 80,551%             66,7076%           

Sum                 517,0               893,0               

------------------------------------------------------------

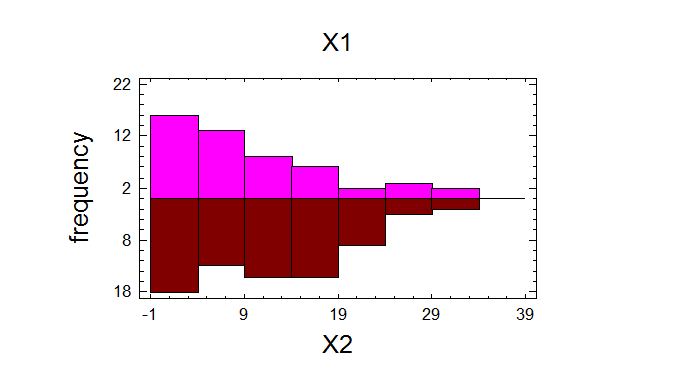
Comparison of Means

-------------------

95,0% confidence interval for mean of X1: 10,34 +/- 2,36707   [7,97293,12,7071]

95,0% confidence interval for mean of X2: 11,9067 +/- 1,82744   [10,0792,13,7341]

95,0% confidence interval for the difference between the means

   assuming equal variances: -1,56667 +/- 2,92685   [-4,49352,1,36019]

t test to compare means

   Null hypothesis: mean1 = mean2

   Alt. hypothesis: mean1 NE mean2

      assuming equal variances: t = -1,05954   P-value = 0,291429

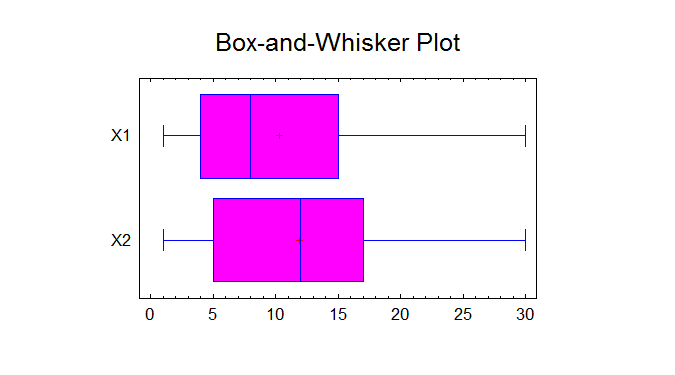
Comparison of Standard Deviations

---------------------------------

                    X1                  X2                 

------------------------------------------------------------

Standard deviation  8,32898             7,94265

Variance            69,3718             63,0858

Df                  49                  74             

     Ratio of Variances = 1,09964

Скачать файл