Лічильники. Основні дані про лічильники і їх класифікація, страница 9

Поліноміальні лічильники (зсуваючі регістри з лінійними зворотними зв'язками, генератори псевдовипадкових послідовностей, лінійні автомати на основі регістрів, що зрушують,) використовуються в пристроях тестового діагностування цифрових пристроїв, для рішення математичних задач методом Монте-Карло, при моделюванні систем з урахуванням випадкового розкиду їхніх параметрів і в ряді інших випадків, наприклад/для надання слова тому чи іншому оратору при обмеженості можливостей засідання.

Ряд назв, що відносяться до поліноміальних лічильників, зв'язаний з поняттям лінійних комбінаційних функцій, лінійних автоматів і т.п. По визначенню до лінійних перемикальних функцій відносяться ті, для яких поліном Жегалкіна має ступінь не вище першої. Такі функції містять конюнкции одиничної довжини і можуть бути представлені у виді

f(x ₁,..., x _N) = а₀Åа₁x₁Åа₂ x₂Å...Åа_n x _n

де а; приймають значення 0 чи 1 (і = O...n).

Автомат є лінійним, якщо схеми вироблення функцій виходів і функції порушення D-тригерів, що утворять пам'ять автомата, є лінійними (ці схеми складені тільки із суматорів по модулю 2).

Можлива реалізація автономного лінійного автомата — регістр, що зрушує, зі зворотними зв'язками через суматори по модулю 2. Такі автомати застосовуються в генераторах псевдовипадкових послідовностей і пристроях тестового контролю ЦУ, де вони забезпечують одержання циклічних кодів.

Випадкові сигнали можуть бути аналоговими чи цифровими. Цифровий сигнал при цьому представляється випадковою послідовністю, елементами якої можуть бути символи 0 і 1 чи багаторозрядні числа. Першому варіанту звичайно привласнюється найменування випадкової послідовності, другому — випадкових чисел.

Випадкові сигнали характеризуються законами розподілу, серед яких важливе місце займає рівномірний закон, тому що сигнали з таким законом розподілу мають не тільки безпосереднє застосування, але і служать для одержання сигналів з іншими законами розподілу шляхом визначеної математичної обробки.

Істинно випадкові послідовності і числа генеруються на основі фізичних явищ (флуктуаціоних шумів і електронних приладів, радіоактивного випромінювання й ін.), що складно реалізується і не забезпечує стабільності статистичних характеристик.

При генерації псевдовипадкових послідовностей і чисел сигнал детерміновано, але його характеристики близькі до характеристик істинно випадкового сигналу. Генерація псевдовипадкових сигналів простіше і надійніше.

Структура регістра, що зрушує, з лінійним зворотним зв'язком показаний на рис. 3.57. Вихідна послідовність знімається з входу тригера d1, вони же повторюється зі зрушеннями в інших крапках тракту, утвореного D-тригерами. Аргументами лінійної функції є величини, що розрізняються тільки зрушеннями на те чи інше число тактів, що відзначається показником ступеня при аргументі х. Структурі схеми ставиться у відповідність поліном

F(x) == хⁿ + a ₁x^n-1 +...+ a_n-1x + 1.

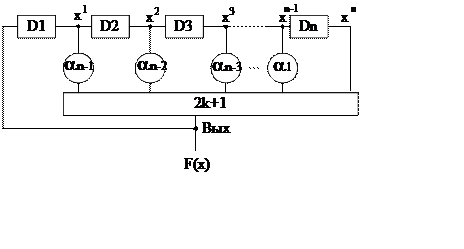
Рис. 15.

Почавши з будь-якого вихідного стану, можна обчислити наступні. На вході лівого тригера виявиться значення функції F(x), що відповідає вихідному стану, в інші — результат зрушення на один розряд. Як тільки знову виникає стан, ідентичне вихідному, усіх почне повторюватися, тобто пристрій працює періодично. Період послідовності залежить від коефіцієнтів a_i. Звичайно бажаний максимальний період. Автомат з n-тригерами може мати 2" станів. У даному автоматі стан усіх нулів повинний бути виключено, тому що з нього схема ніколи не зможе вийти. Тому для даного автомата максимальний період складе 2ⁿ—1, а відповідна йому послідовність називається послідовністю максимальної чи довжини М-послідовністю.

До М-послідовності приводять багато варіантів схеми. Їхній пошук заснований на вивченні полінома, що відповідає схемі. Щоб генерувалася М-послідовність, поліном повинний бути, що не приводиться і примітивним. Таких поліномів багато: при n = 8 їх 16, при n == 16 уже 2048 і м. д. Серед безлічі поліномів доцільно відшукати такі, у яких мінімальне число ненульових коефіцієнтів a оскільки це спрощує схему.