Лічильники. Основні дані про лічильники і їх класифікація, страница 5

При розробці деяких схем у них уводять спеціальні чи елементи підсхеми для додання властивостей самозапуску. Діаграма станів лічильника з модулем 5 представлена на рис. 8.

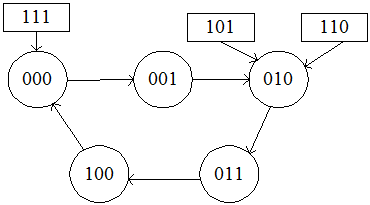
Рис. 8.

Серед лічильників з довільним модулем особливе місце займають двоїчно-десяткові, що мають модуль 10. У серіях ИС нерідко реалізують ідентичні по інших ознаках лічильники з модулями 16 і 10. Лічильник з модулем 10 неважко побудувати формально проілюстрованим вище методом.

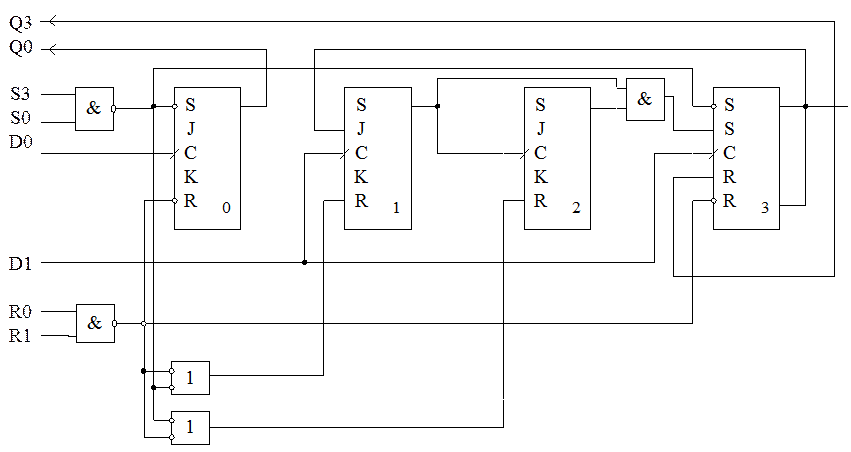
Рис. 9.

Схема лічильника ИЕ2, що з'явилася в найперших серіях ИС і дотепер повторюється в усіх більш нових ,(рис. 9), складається фактично з двох секцій з модулями 2 і 5, представлених тригером Те і групою Т₁Т₂Т₃, на якій зібраний лічильник з модулем 5. Секції можна використовувати по чи окремості з'єднувати послідовно за допомогою зовнішньої комутації висновків для одержання двоїчно-десяткового лічильника. Мається скидання по конюнкції сигналів R₀R₁ і установка в стан 1001 по конюнкції сигналів S₀S₁. Режими невикористовуваних входів не показані. З'єднання лічильників у порядку mod2-rnod5 дає двоїчно-десятковий лічильник із природною послідовністю рахунка, що у режимі дільника частоти формує імпульси зі шпаруватістю 5. З'єднання в порядку mod5-mod2 дає, природно, той же модуль рахунка, але стану лічильника утворять послідовність чисел 0, 1,2, 3, 4, 8, 9, 10, 11, 12, після якого цикл повторюється. У режимі дільника частоти формуються імпульси зі шпаруватістю 2. Таким чином, розбивка лічильника на двох секцій надає можливість одержати як звичайний двоїчно-десятковий лічильник, так і два дільники частоти на 10— з формуванням вузьких імпульсів ((і = Т/5) і симетричних імпульсів ((і = Т/2), де Т — період повторення імпульсів.

Поряд із секціонованим двоїчно-десятковим лічильником, у серіях ИС маються і звичайні з різними сполученнями класифікаційних ознак (до 5...10 варіантів).

1.6.2. Побудова лічильника другим способом

Другий метод побудови лічильників з довільним модулем — метод керованого скидання— дозволяє змінювати модуль рахунка дуже простим способом, що не вимагає змін самої схеми лічильника.

Розглянемо цей спосіб стосовно до реалізації синхронного лічильника з рівнобіжним переносом. Функції порушення двоїчного лічильника зазначеного типу, як відомо, мають вид J_i = К_i = Q₀Q₁.. Q_i-1 (у молодшому тригері j₀ = ДО₀ = 1). Введемо в ці функції сигнал скидання R, змінивши їх у такий спосіб:

J_i=(Q₀Q₁-Q_i-1)R, К_i = j_ivr.

Рис. 10.

Поки сигнал скидання відсутній (R = 0), функції J_i і К_i не відрізняються від відповідних функцій двоїчного лічильника. Коли сигнал R здобуває одиничне значення, усі функції J_i, стають нульовими. К_i — одиничними, що змушує всі тригери скинутися по приходу наступного такту.

Якщо сигнал R з'явиться як наслідок появи в лічильнику числа М-1, то буде реалізована послідовність рахунка 0, 1, 2,..., M-l, 0..., тобто лічильник з модулем М.

Схеми всіх розрядів лічильника з керованим скиданням не залежать від модуля рахунка. Крім розрядних схем, лічильник містить один конюнктор, що виробляє сигнал скидання при досягненні вмістом лічильника значення М-1 (рис. 9, а).

Якщо, наприклад, мається чотирьохрозрядний лічильник, і на входи конюнктора вироблення сигналу скидання підключені виходи тригерів, як показано на рис. 9, б, то скидання відбудеться після досягнення лічильником числа 1001 = 9, тобто лічильник буде працювати як двоїчно-десятковий.

                      1.7. Лічильники з недвійковим кодуванням

Найбільше практичне значення серед лічильників з недвійковим кодуванням станів мають лічильники з кодом Гріючи, лічильники Джонсона і лічильники з кодом "1 з N".

1.7.1. Лічильники в коді Грея