Статистическое моделирование псевдослучайных последовательностей, страница 3

3. Определить выборочное среднее и среднеквадратическое отклонение полученной последовательности, построить автоковариационную функцию.

Выборочное среднее:

Среднеквадратичное отклонение:

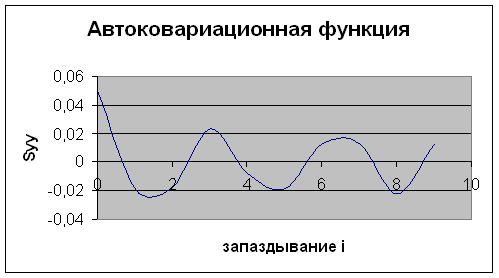
Автоковариационная функция:

i = -m,…0,…m,

где   - время сдвига.

4. Построить гистограмму псевдослучайной выборки и проверить согласие теоретического и экспериментального законов распределения по критерию .

Количество интервалов гистограммы:

n = E{1+3,22lgN} = E{1+3,22lg90} = 7

Ширина интервалов:

Частота попадания СВ в j-ый интервал определяется по формуле:

, где N_j – количество попаданий СВ в j-ый интервал.