|
||||||
|
||||||
|
||||||
|
||||
|
||||
ЗАДАЧА № 1
Зважений граф інформаційної залежності щодо побудування паралельного алгоритму обчислювальної задачи надан базовою матрицею iнциденцiй і базовою таблицею вагів вершин у слідуючому вигляді:
Базова матриця інциденцій вершин:
|
Вершина початку ребра |
8 |
1 |
8 |
8 |
1 |
5 |
3 |
3 |
6 |
7 |
4 |
|
Вершина кінця ребра |
4 |
4 |
5 |
3 |
7 |
2 |
6 |
7 |
2 |
2 |
2 |
Таблиця вагів вершин:
|
Номер вершини |
8 |
1 |
5 |
3 |
4 |
6 |
7 |
2 |
|
Вага вершини |
2 |
3 |
5 |
2 |
4 |
3 |
2 |
1 |
Виконати формальний аналiз iнформацiйної незалежності операторiв:
1) Виконати лексікографічне упорядкування наданого графа
2) Обчислити час раннього термiну закiнчення виконання операторiв
3) Знайти критичний час виконання алгоритму Ткр за означеним графом
4) Приймаючи час виконання
усього набору операторiв найменьшим за 
одиниць,
обчислити час пiзнього термiну закiнчення виконання операторiв.
5) Відзначити на часових діаграмах інтервали можливого запуску і часу воконання кожного з операторів.
6) Побудувати графіки щільності навантаження процесорів для моменту раннього і пізнього термінів
7) Побудувати діаграму розмiщення iнтервалiв допустимого закiнчення виконання операторiв по паралельних гiлках, розташованих у двох процесорах.
1. Виконати лексікографічне упорядкування наданого графа. Згідно з варіантом за таблицею матриці інциденцій складаємо впорядкований граф (Рисунок 1).
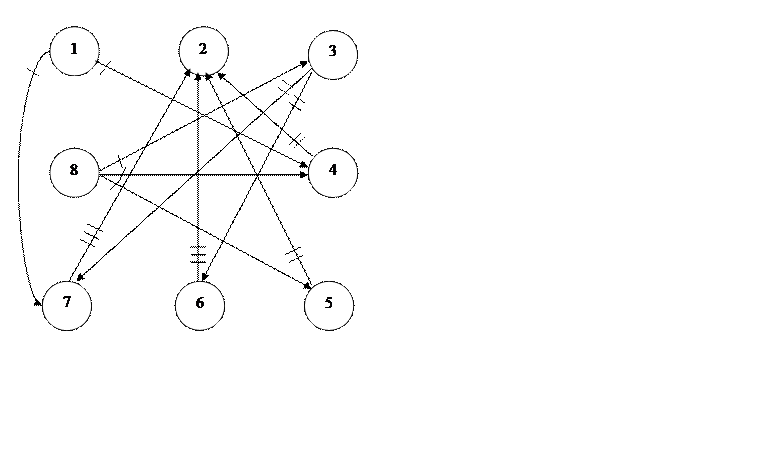
Початкова вершина графа – це така вершина з якої виходять всі дуги (у даному випадку 1 та 8), а кінцева – та у яку надходять усі дуги (у даному випадку 2). Початкові вершини будуть находитись на першому ярусі а кінцева на останньому (четвертому). Після розподілення вершин графу по ярусам отримуємо рисунок 2.
|
|
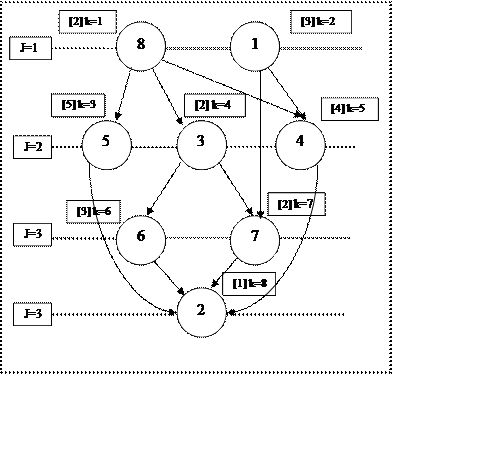
Список вершин з множиною дуг.
|
Ім’я вершини |
δ+(vi), множина дуг які виходять з вершини |
δ-(vi), множина дуг які входять до вершини |
Ярус (j) |
Новий індекс (К) |
|
8 |
{5,3,4} |
{0} |
1 |
1 |
|
1 |
{4,7} |
{0} |
1 |
2 |
|
5 |
{2} |
{8} |
2 |
3 |
|
3 |
{6,7} |
{8} |
2 |
4 |
|
4 |
{2} |
{1,8} |
2 |
5 |
|
6 |
{2} |
{3} |
3 |
6 |
|
7 |
{2} |
{3,4} |
3 |
7 |
|
2 |
{0} |
{4,5,6,7} |
4 |
8 |
Матриця суміжності для графу.
Матриця суміжності містить з’єднання вершин графу. «1» - ребро виходить з вершини. «-1» - входить до вершини.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
3 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
|
4 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
5 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
6 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
7 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
8 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
S =
Упорядкована матриця суміжності для графу.
Sy =
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
