Исследование точности работы САУ и их элементов в установившихся и переходных режимах. Вариант № 4, страница 2

11

---

s^2

>> W2i1=feedback(W2i, 1)

Transfer function:

   11

--------

s^2 + 11

>> W2i2=feedback(W2i, 0.2)

Transfer function:

   11

---------

s^2 + 2.2

>> W2i3=feedback(W2i, 0.1)

Transfer function: 

11

---------

s^2 + 1.1

Построение переходных характеристик двойного интегратора

Без ОС:

>> step(W2i)

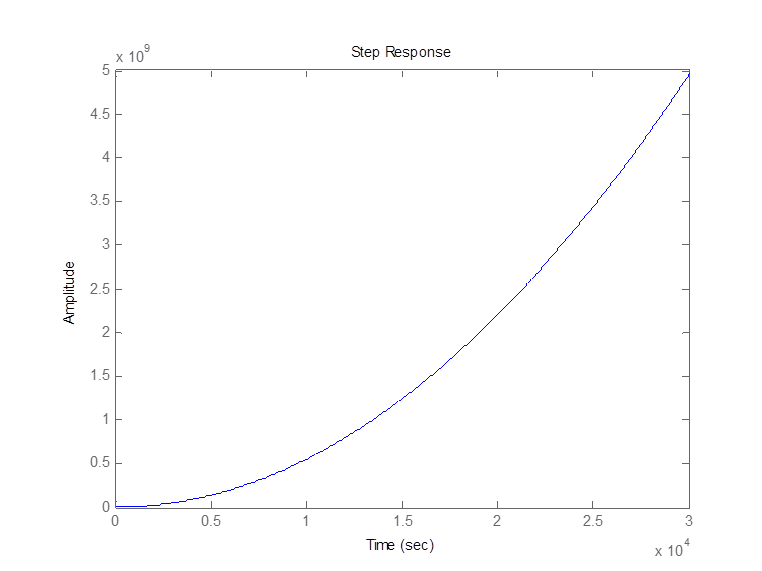
С введенной ОС:

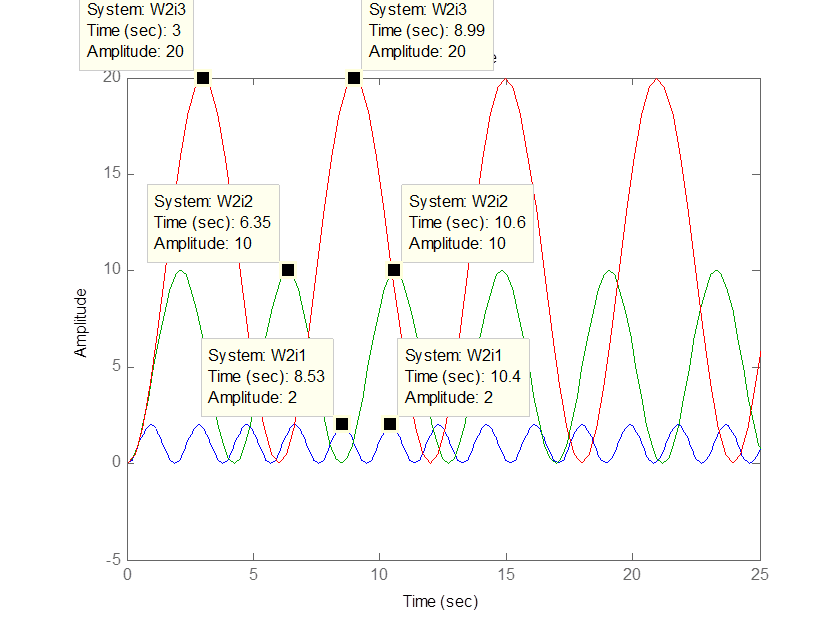
Амплитуды:  

Частоты:

 

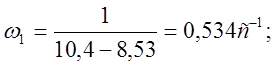
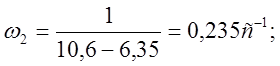
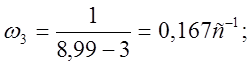
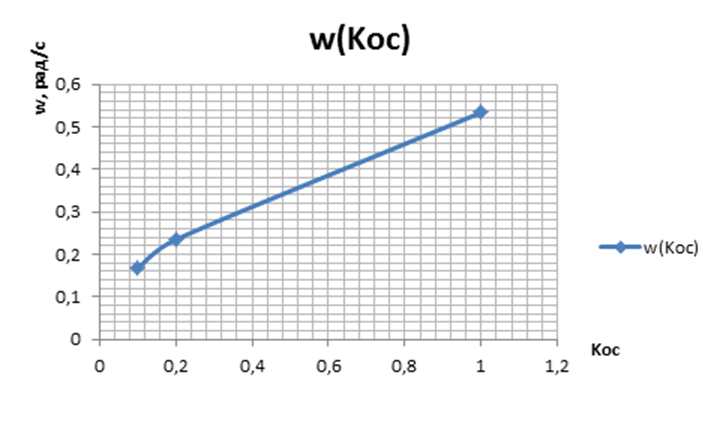
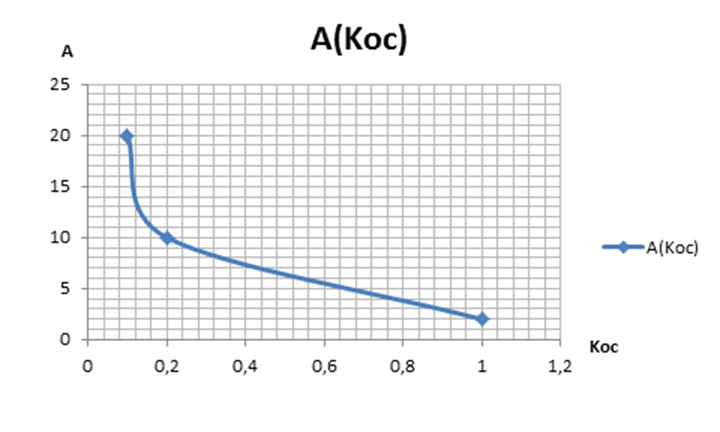
Построим зависимости  

2. Исследование точности систем при

обработке типовых управляющих воздействий.

1) Точность при отработке единичного ступенчатого воздействия.

Запишем ПФ разомкнутых систем с астатизмом различного порядка:

n = 0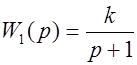          

n = 1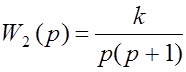           

n = 2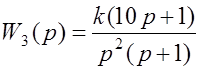           

>> k=4.2;

Передаточная функция разомкнутой системы с астатизмом :

>> W1=tf(k,[1 1])

Transfer function:

 4.2

-----

s + 1

Передаточная функция разомкнутой системы с астатизмом :

>> W2=tf(k,[1 1 0])

Transfer function:

  4.2

-------

s^2 + s

Передаточная функция разомкнутой системы с астатизмом :

>> W3=tf([10*k k],[1 1 0 0])

Transfer function:

42 s + 4.2

----------

s^3 + s^2

Получим ПФ замкнутых систем:

>> Wz1=feedback(W1,1)

Transfer function:

  4.2

-------

s + 5.2

>> Wz2=feedback(W2,1)

Transfer function:

     4.2

-------------

s^2 + s + 4.2

>> Wz3=feedback(W3,1)

Transfer function:

      42 s + 4.2

----------------------

s^3 + s^2 + 42 s + 4.2

Получение на одном графике ПХ замкнутых систем для трёх ПФ:

>> step(Wz1,Wz2,Wz3)

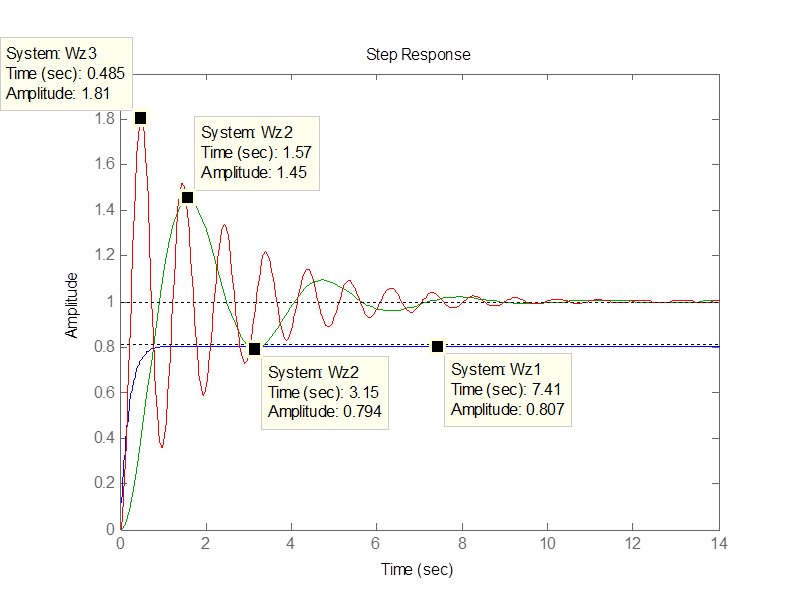
В установившемся состоянии для звеньев с астатизмом первого и второго порядка статическая ошибка равна нулю. Для звена с астатизмом нулевого порядка статическая ошибка составляет:

          Для звена с астатизмом нулевого порядка, замкнутого отрицательной обратной связью характерен апериодический переходный процесс; для звена астатизмом первого порядка колебательный переходный процесс с коэффициентом демпфирования ; для звена астатизмом второго порядка так же колебательный переходный процесс.

2) Точность при отработке единичного скачка скорости.

Умножим каждую из передаточных функций  на 1/р:

>> w=tf(1,[1 0])

Transfer function:

1

-

s

>> w1=Wz1*w

Transfer function:

    4.2

-----------

s^2 + 5.2 s

>> w2=Wz2*w

Transfer function:

       4.2

-----------------

s^3 + s^2 + 4.2 s

>> w3=Wz3*w

Transfer function:

        42 s + 4.2

--------------------------

s^4 + s^3 + 42 s^2 + 4.2 s

Для данных звеньев построим передаточные характеристики:

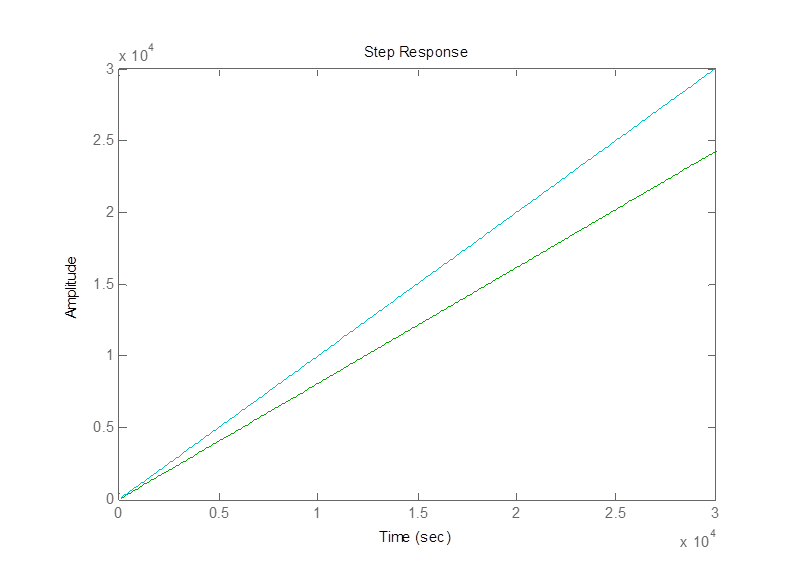
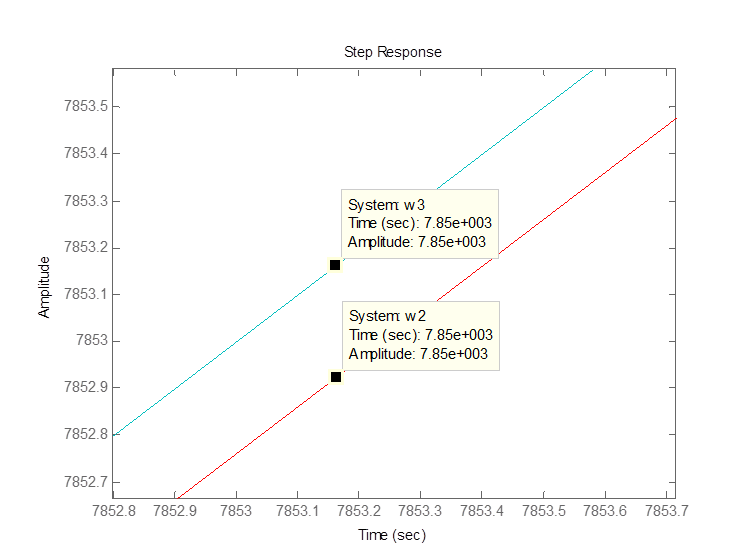
3) Точность при отработке единичного скачка ускорения.

Преобразуем все 4-е ПФ: W, W1, W2, W3 умножением каждой на 1/p.

>> w11=w1*w

Transfer function:

     4.2

-------------

s^3 + 5.2 s^2

>> w22=w2*w

Transfer function:

        4.2

-------------------

s^4 + s^3 + 4.2 s^2

 >> w33=w3*w

Transfer function:

         42 s + 4.2

----------------------------

s^5 + s^4 + 42 s^3 + 4.2 s^2

>> w44=w*w

Transfer function:

 1

---

s^2

>> step(w44,w11,w22,w33)

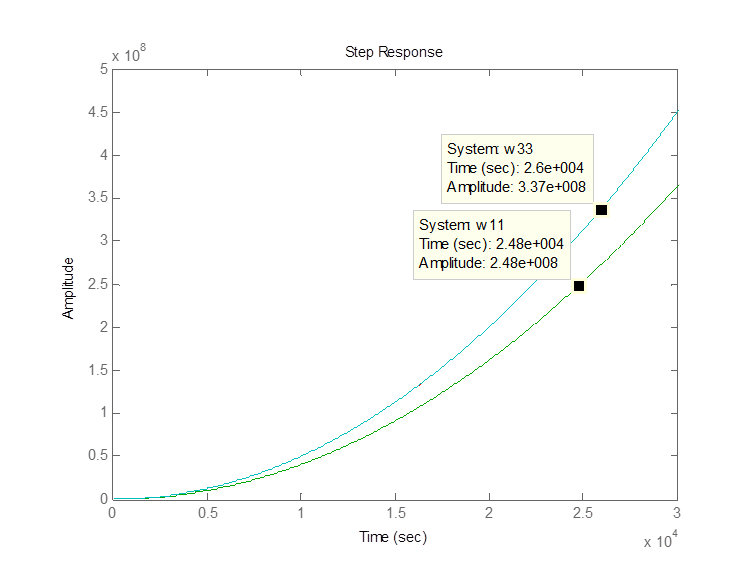
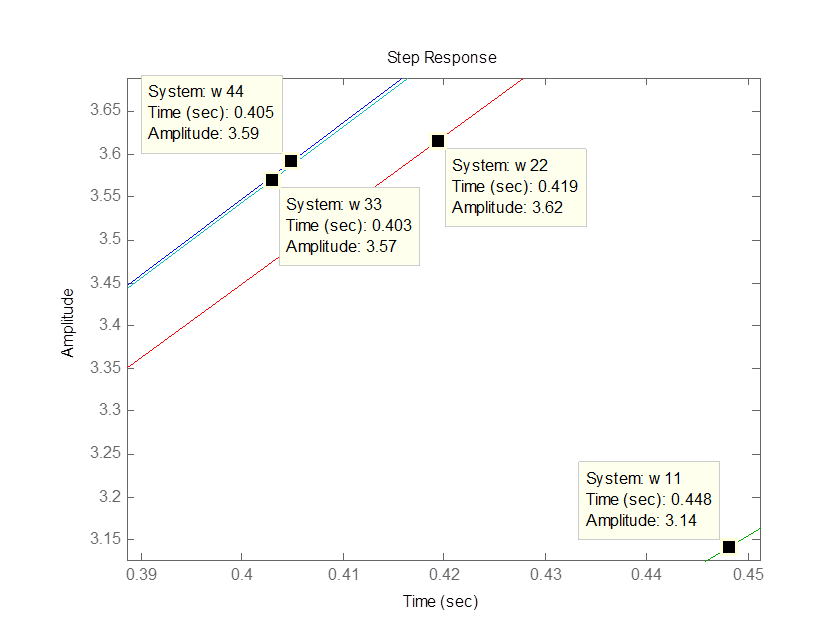
3.Исследование точности систем
при отработке типовых возмущающих воздействий

Определим ПФ замкнутых систем по возмущающему воздействию и ввести их в ПК.

 

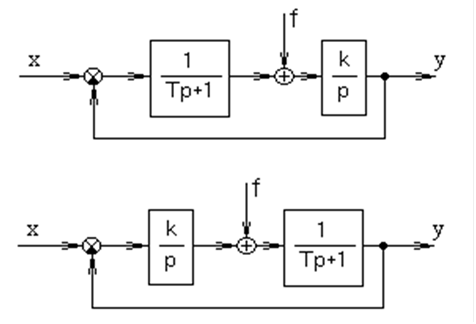a)

б)

э=

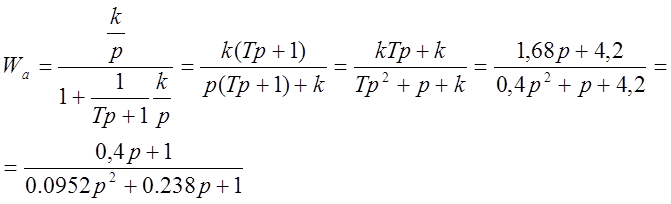
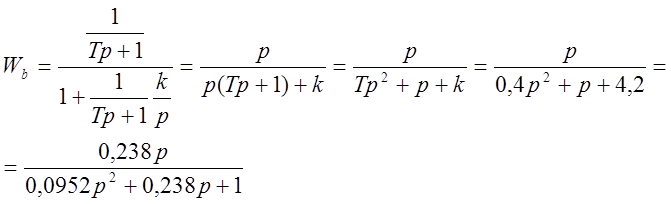
Постоянные времени: Т_а1 = 0,0952; Т_а2 = 0,238.

>> Wa=tf([0.4 1],[0.0952 0.238 1])

Transfer function:

       0.4 s + 1

------------------------

0.0952 s^2 + 0.238 s + 1

>> Wb=tf([0.238 0],[0.0952 0.238 1])

Transfer function:

        0.238 s

------------------------

0.0952 s^2 + 0.238 s + 1

>> step(Wa,Wb)

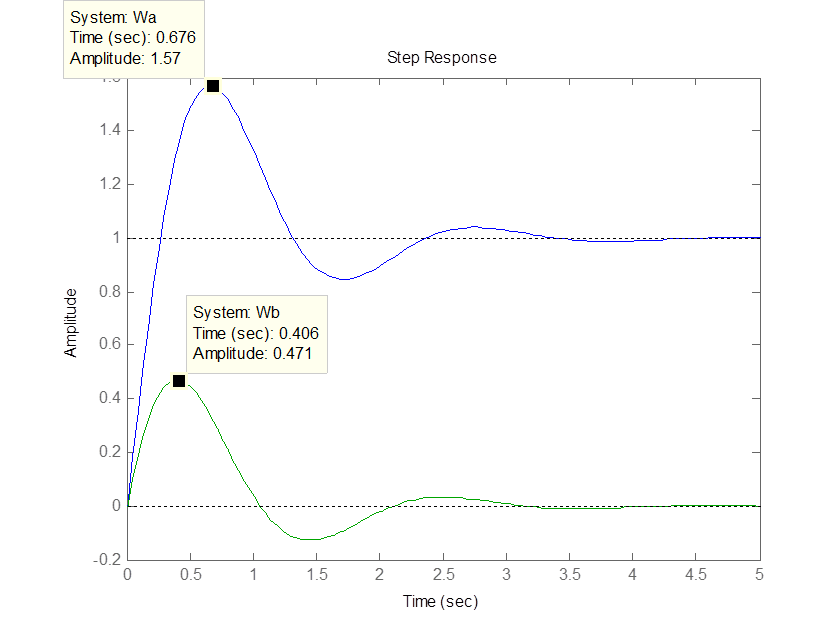
Для системы (а) в установившемся режиме после подачи возмущающего воздействия устанавливается статическая ошибка, величина которой равна 1 (данная система имеет астатизм нулевого порядка). Система (б) после подачи возмущающего воздействия возвращается в своё первоначальное состояние (данная система имеет астатизм первого порядка, так как содержит звено интегрирования в канале обратной связи относительно возмущающего воздействия).