Методика аналогового моделирования динамических объектов, страница 6

Рис. 3.9. Схема реализации звена.

 где

Постоянные времени отосятся к различным группам реализации однако, при различии всего на порядок, можно проводить реализацию такого звена быз разделения, так как звено имеет высший порядок 2.

Используя соотношени для постоянных времени звена, можно записать:

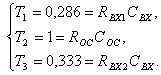
Так как имеем пять неизвестных в трёх уравнениях, то необходимо выбрать номинал какого-либо из элементов, при помощи которого проводится дальнейший расчет. Выберем номиналы конденсаторов ( как наиболее требовательных, кроме ОУ, элементов)  и  одинаковыми.

Делаем так для упрощения примера – при реализации можно использовать различные номиналы, но не расходящиеся на много порядков (почему, объеснялось выше):  мкФ,  мкФ. Следовательно, представленная выше система уравнений примет вид:

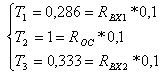
Далее не составляет труда найти номиналы резисторов:

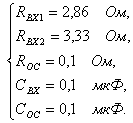
Но не учтён коэффициент . Он реализуется отдельно звеном “масштабирующий усилитель” (см. Глава 2, п. 2.1.1):

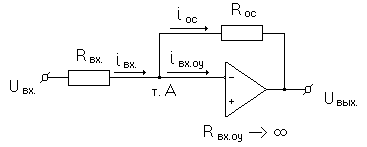
Рис. 3.10. Схема реализации звена.

Номиналы схемы которого расчитываются по формуле: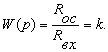

Также как и при реализации основного звена, необходимо выбрать один из элементов. Можно выбирать входное сопротивление как расчётное, так как оно обычно имеет номинал равный входному сопротивлению ОУ, но это не правило и не требование, а практика. Выберем номинал входного резистора  Ом, как более близкий к номиналам резисторов первой схемы.                                    Тогда  Ом.

Теперь можно составить конечную схему модели:

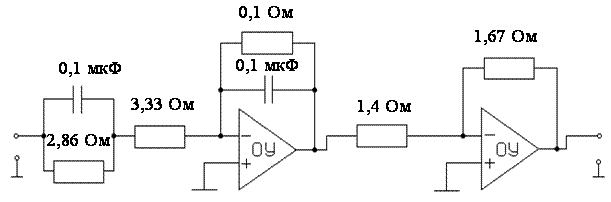
Рис. 3.11. Схема аналоговой модели исходной системы.

Пример 2: Исходные данные:

Система линейная замкнутая, передаточная функция: .

Задача: составить аналоговую модель системы.

Аналогичным с первым примером образом проводим анализ системы:

Замечаем, что постоянные времени относятся к одной порядковой группе, а звено можно представить последовательным соединением дифференцирующего и инерционного (см. Глава 2, п. 2.1.9) звеньев:

 

Рис. 3.12. Схема реализации звена.

Расчитать номиналы элементов можно по формулам:

 где

Получаем систему:

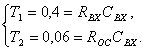
Вновь задаёмся номиналом конденсатора .

Система примет вид:

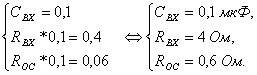
При постаноки задачи для незамкнутой системы на этом можно было бы завершить расчёты и преступить к составлению схемы, но в данном случае система замкнута и необходимо провести расчёт сумматора. Расчёт, в данном случае сведётся к анализу – так как в исходных данных ничего не сказано про коэффициент умножения, которым может обладать сумматор, то принимаем  этот коэффициент равным 1, тогда: